Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 30
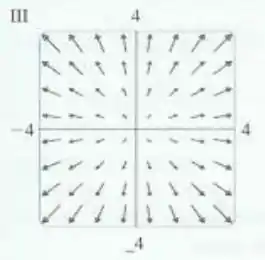
Faça uma correspondência entre as funções e os desenhos de seus campos vetoriais gradientes (rotulados de ). Justifique suas escolhas.
Passo 1
Galera, vamos lembrar do seguinte:
Então, é só calcular as derivadas parciais de :
Ou seja,
Passo 2
Show! Perceba que a componente vertical dos vetores do campo vetorial gradiente obtido vai depender somente de . Então, quando , os vetores terão componente vertical para cima, e quando , para baixo. Ou seja, isso parece corresponder a:
Resposta
Exercícios de Livros Relacionados
Determine o campo do vetor gradiente ∇ f de f e o desenhe. f x , y = 1 4 x + y 2
Case as funções com os desenhos de seus campos de vetor gradiente (rotulados de I-IV). Dê razões para suas escolhas. f x , y = x 2 - y 2
Determinar r o tf → sendo: f → = 2 x 2 yi → + 3 x zj → - yk →
Sejam f → = ( x z ,z y ,x y ) e g → = x 2 ,y 2 ,z 2 . Determinar: ∇ × g →
Encontrar a divergência e o rotacional do campo vetorial dado. f → x ,y ,z = x y 2 z i → + 2 j → + 3 k →