Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 29
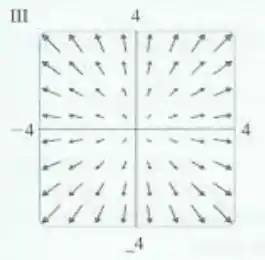
Faça uma correspondência entre as funções e os desenhos de seus campos vetoriais gradientes (rotulados de ). Justifique suas escolhas.
Passo 1
Galera, vamos lembrar do seguinte:
Então, é só calcular as derivadas parciais de :
Ou seja,
Passo 2
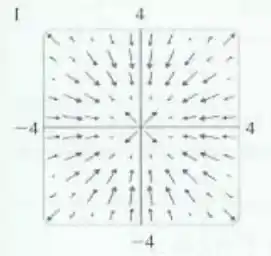
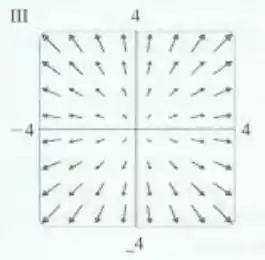
Show! O campo vetorial gradiente obtido no passo anterior mostra que os vetores vão apontar pra longe da origem, com magnitude que vai aumenta à medida que a distância do ponto até a origem aumenta.
Então, a nossa única possibilidade é:
Resposta
Exercícios de Livros Relacionados
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = z j
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = y j
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = j - i
Case as funções com os desenhos de seus campos de vetor gradiente (rotulados de I-IV). Dê razões para suas escolhas. f x , y = x 2 + y 2
Determine o campo do vetor gradiente ∇ f de f e o desenhe. f x , y = x y - 2 x