Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 31
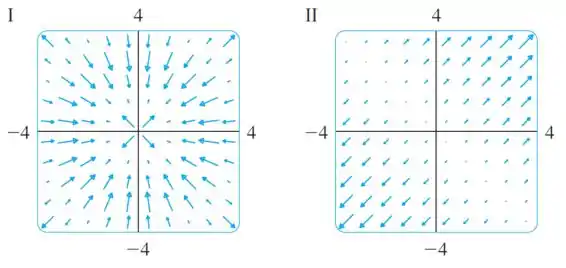
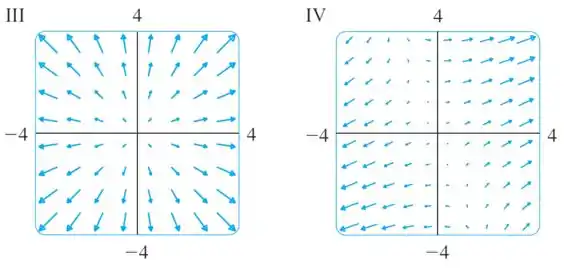
Faça uma correspondência entre as funções e os desenhos de seus campos vetoriais gradientes (rotulados de ). Justifique suas escolhas.
Passo 1
E aii, galera!
Nessa questão temos uma função de duas variáveis:
E temos que descobrir qual das quatro imagens que ela deu representa o campo vetorial gradiente dela.
Pra isso, vamos primeiro calcular o gradiente, que é:
E então estudar como ele se comporta de acordo com o ponto , pra relacionar com um dos campos desenhados.
Passo 2
Primeiro, vamos calcular a derivada em função de , considerando constante:
E em função de , com constante:
Então o campo gradiente é:
Passo 3
Agora percebe que as duas componentes dos vetores do campo gradiente são iguais!
Bom, os vetores vão ter essa característica:
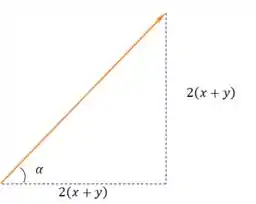
Como esse triângulo é retângulo, temos que:
Ou seja, todos os vetores têm essa angulação, e são paralelos à reta .
A única imagem que tem os vetores assim é a .