Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 32
Faça uma correspondência entre as funções e os desenhos de seus campos vetoriais gradientes (rotulados de ). Justifique suas escolhas.
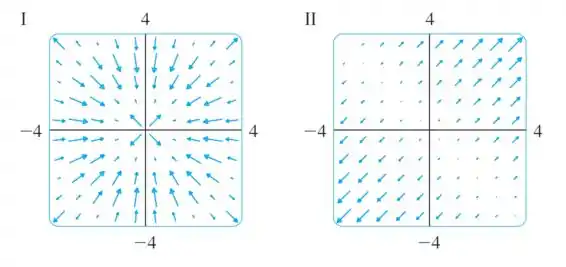
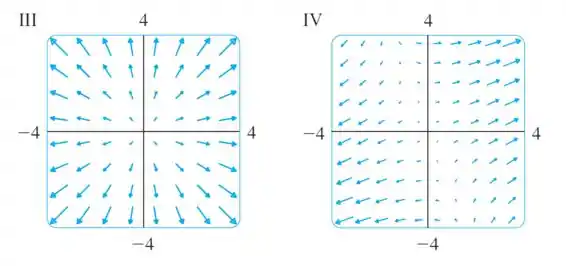
Passo 1
E ai, galera, tudo certo?
Nessa questão, temos uma função
E queremos descobrir qual dessas quatro figuras representa o seu campo vetorial gradiente.
Pra isso, vamos lembrar que o gradiente é calculado assim:
Então a primeira coisa vai ser calcular as derivadas parciais de , daí teremos o campo gradiente e vemos como ele se comporta, comparando com as opções que a questão deu!
Nessa análise, vamos precisar estudar os tamanhos dos vetores, que são dados pela norma:
Passo 2
Calculando as derivadas parciais.
Primeiro em função de , considerando como constante:
Temos que usar a regra da cadeia duas vezes, já que temos uma composição de três funções:
Então:
Para a derivada em função de o processo vai ser o mesmo, só que agora é constante:
De novo usando regra da cadeia duas vezes:
Então:
Ou seja,
Passo 3
Vamos calcular a norma desses vetores:
Podemos colocar o cosseno e o denominador em evidência:
Pra tirar esse cosseno da raiz, temos que colocar um módulo, então:
Passo 4
Agora a gente precisa prestar atenção nessa fórmula da norma pra perceber duas coisas muito importantes:
Primeiro:
Como cosseno é uma função periódica, sabemos que os tamanhos dos vetores vão ficar aumentando e diminuindo, conforme o cosseno aumenta e diminui...
Segundo:
Como o argumento do cosseno é
Isso quer dizer que se dois pontos tem o mesmo valor dessa expressão, eles terão o mesmo tamanho. Só que essa expressão representa exatamente a distância de um ponto até a origem.
Tá, mas e daí??
Bom, isso quer dizer que pra uma distância , todos os pontos que estão a essa distância da origem terão vetor do mesmo tamanho! Mas os pontos que têm uma mesma distância até a origem formam uma circunferência! Não é a toa que a equação da circunferência é
Esse é exatamente a distância !
CONCLUSÃO...
No nosso campo vetorial, os pontos que fazem parte de uma mesma circunferência terão vetores de mesmo tamanho, e conforme essa circunferência aumenta, os tamanhos vão aumentando e diminuindo.
A primeira parte dessa conclusão nos levaria a ficar na dúvida entre e :
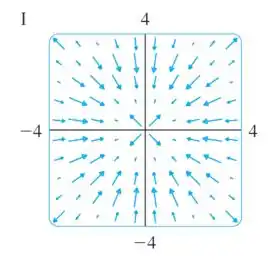
Mas na figura os tamanhos dos vetores só aumentam.
Então nossa resposta é figura .