Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.3 - Ex. 1
Faça um desenho para mostrar que
O que você pode concluir sobre a série?
Passo 1
Olá, amigos! Tudo certo?
Bom, vamos começar entendendo nossa questão.
Um desenho que podemos trazer é o gráfico das áreas embaixo da curva (ou seja, da integral) da função e aí comparamos o valor de cada integral de dos intervalos de 1 em 1, com cada termo da série, que também simboliza as áreas do retângulos dos intervalos de 1 em 1.
Quando ele pergunta para nós o que podemos concluir da série, podemos analisar se nossa série converge ou diverge.
Bom, no geral para determinar a convergência ou divergência de uma série poderíamos usar o Teste da Integral. Porém, nesse caso, o que temos é uma série do tipo p-série.
A vantagem disso é que para a p-série (ou série-p), basta analisarmos o valor de para entender se há convergência ou divergência. Viu como fica muuuuuito mais fácil que calcular integrais? Vamos lá, então!
Para a série-p, temos:
- É convergente se
- É divergente se
Passo 2
Galera, vamos fazer o seguinte desenho:
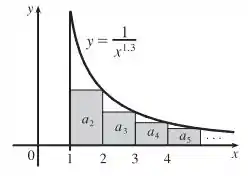
Vamos começar entendendo alguns conceitos. Vamos pegar o intervalo de 1 até 2 como exemplo.
A integral significa a área embaixo da curva no intervalo 1 a 2. Já , como podemos ver no desenho é o retângulo de base 1 e altura . Perceba ali no desenho como o retângulo deixa um “espaço em branco”. Ele não pega toda a área embaixo da curva. Então o valor de vai ser menor que o valor real que temos abaixo da curva, que é .
Por isso podemos dizer que:
E assim para os demais intervalos:
e assim por diante, de forma que chegamos a:
Passo 3
Show! Agora vamos calcular a integral, para descobrirmos se a série converge ou diverge:
Nossa série-p é:
Vemos aqui que . Como nosso , nossa série converge.
Resposta
Série convergente.