Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 90

(a) A sequência a n é definida recursivamente pela equação a n = 1 2 a n - 1 + a n - 2 para n ≥ 3 , onde a 1 e a 2 podem ser quaisquer números reais. Experimente com vários valores de a 1 e a 2 e use sua calculadora para descobrir o limite da sequência.

(b) Encontre lim n → ∞ ⁡ a n em termos de a 1 e a 2 expressando a n + 1 - a n em termos de a 2 - a 1 e somando uma série.

Passo 1

Pesssoal, aqui temos a seguinte sequência:

a n = 1 2 a n - 1 + a n - 2

Os primeiros 2 termos podem variar, e depois seguem essa lei.

Pro item a, vamos montar uma tabela com a sequência pra diferentes valores de a 1 e a 2

No item b vamos achar uma expressão pra a n e depois calcular:

lim n → ∞ ⁡ a n

Passo 2

Galera, usando uma calculadora, podemos calcular vários termos da sequência a n , definindo diversos valores para a 1 e a 2 , conforme mostra a tabela a seguir:

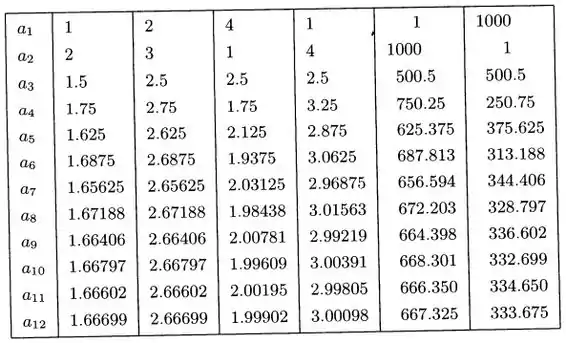
Os limites parecem ser 5 3 , 8 3 ,   2 ,   3 ,   667 e 334 , com base nos valores de a 12 . Então a gente consegue chutar um valor geral para o limite:

lim n → ∞ ⁡ a n = a 1 + 2 a 2 3

Passo 3

(b) Vamos tentar encontrar formalmente o limite da sequência. Começamos tentando expressar a n + 1 - a n em termos de a 2 - a 1 .

Sabemos que

a n = 1 2 a n - 1 + a n - 2

Então:

a n + 1 = 1 2 a n + a n - 1

Substituindo:

a n + 1 - a n = 1 2 a n + a n - 1 - a n = - 1 2 a n - a n - 1

Agora substituindo a n = 1 2 a n - 1 + a n - 2 :

= - 1 2 1 2 a n - 1 + a n - 2 - a n - 1 = - 1 2 - 1 2 a n - 1 - a n - 2 =

E fazendo isso repetidamente, chegamos em:

- 1 2 n - 1 a 2 - a 1

Agora repare que podemos escrever o seguinte:

a n = a 1 + a 2 - a 1 + a 3 - a 2 + … + a n - 1 - a n - 2 + a n - a n - 1

Em forma de somatórios:

= a 1 + ∑ k = 1 n - 1 a k + 1 - a k = a 1 + ∑ k = 1 n - 1 - 1 2 k - 1 a 2 - a 1

Passo 4

Show! Tendo achado uma expressão para a n , podemos calcular o limite:

lim n → ∞ ⁡ a n = lim n → ∞ ⁡ a 1 + ∑ k = 1 n - 1 - 1 2 k - 1 a 2 - a 1

O infinito vai entrar no limite superior do somatório:

= a 1 + ∑ k = 1 ∞ - 1 2 k - 1 a 2 - a 1

Essa é uma série geométrica:

∑ k = 1 ∞ - 1 2 k - 1

Numa série geométrica, a soma é

∑ n = 1 ∞ a r n = 1 1 - r

Então:

∑ k = 1 ∞ - 1 2 k - 1 = a 1 + a 2 - a 1 1 - - 1 2

E finalmente:

= a 1 + 2 3 a 2 - a 1 = a 1 + 2 a 2 3

Achamos nosso resultado!

Resposta

(b) lim n → ∞ ⁡ a n = a 1 + 2 a 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a n -ésima soma parcial de uma série ∑ n = 1 ∞ a n for s n = 3 - n 2 - n Encontre a n e ∑ n = 1 ∞ a n .
A figura exibe dois círculos C e D de raio 1 que se tocam em P . T é uma reta tangente comum; C 1 é o circulo que toca C , D e T ; C 2 é o circulo que toca C , D e C 1 ; C 3 é o circulo que toca C , D
Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequencias de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se for convergente, c
Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequencias de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se for convergente, c
Encontre um valor de n que garanta que o erro na aproximação s ≈ s n seja menor que 0,001 .