Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 3
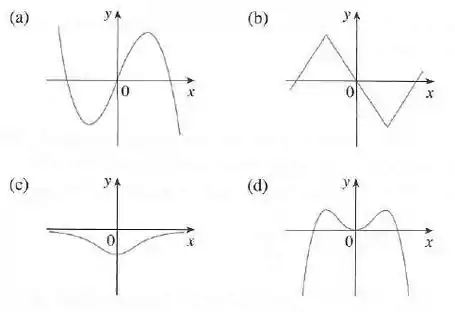
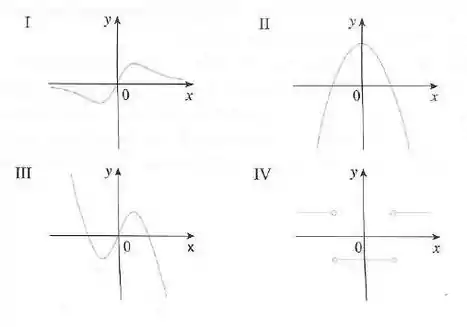
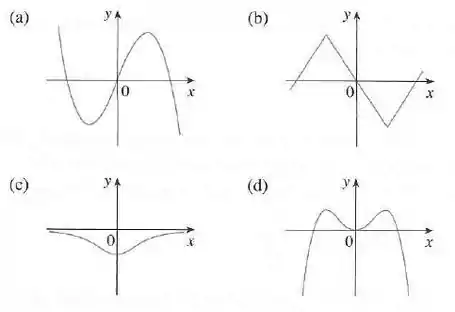
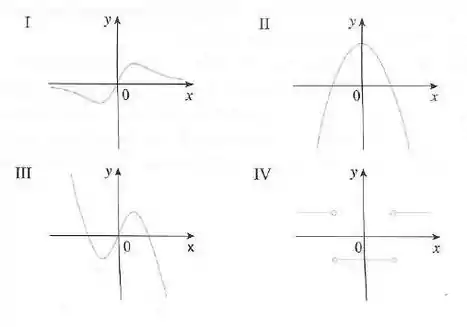
Associe o gráfico de cada função em (a)-(d) com o gráfico de sua derivada em I-IV. Dê razões para suas escolhas.
Passo 1
E aí! tudo certinho? 😐
Nesse problema foi dado alguns gráficos de funções e nosso objetivo é determinar qual é o gráfico correspondente da derivada de cada função.
Olha só os gráficos que temos:
Parece complicado? 👀
Para responder esse problema temos que imaginar como o gráfico da derivada de cada função se comporta a partir do comportamento da função.
Veja só! 😉
Passo 2
Gráfico a)
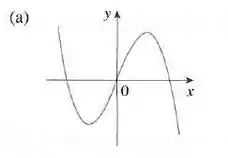
Vamos analisar a partir da esquerda indo pra direita: as inclinações das tangentes do gráfico (a) começam negativas, se torna e depois positivas, de novo e depois negativas novamente.
Também vamos que os valores da função no gráfico II seguem o mesmo padrão.
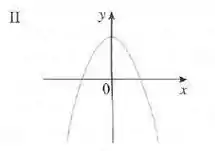
Bacana, não é? 😊
Passo 3
Gráfico b)
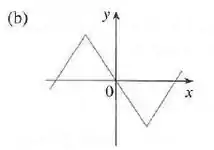
Vemos que a partir da esquerda indo pra direita, as inclinações das tangentes do gráfico (b) começam fixadas em um valor positivo, então de repente se tornam negativas, e ficam positivas de novo. No gráfico IV tambpem temos descontinuidades que indicam mudanças repentinas nas inclinações das tangentes.
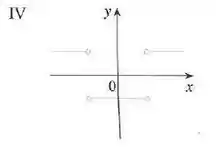
Tranquilo até aqui? 😬
Passo 4
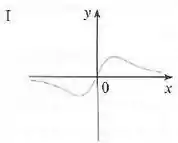
Gráfico c)
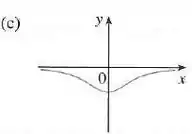
Vemos que as inclinações das tangentes do gráfico (c) são negativas para e positivas para , e os valores das funções do gráfico I também seguem esse padrão.
O que achou? 👀
Passo 5
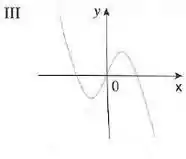
Gráfico d)
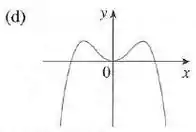
Vemos que a partir da esquerda indo pra direita, as inclinações das tangentes do gráfico (d) são positivas, então , se tornam negativas, volta a ser novamente, então positiva, de novo e por ultimo, ufa, negativa e os valores da função do gráfico III seguem o mesmo padrão.
E fim! Entendeu tudo? Responde Aí! 😉
Resposta
(a)-II
(b)-IV
(c)-I
(d)-III