Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.6 - Ex. 29

Encontre uma fórmula explícita de f - 1 e use-a para fazer na mesma tela os gráficos de f - 1 ,   f e dada a reta y = x . Para verificar seu trabalho veja se seus gráficos de f e f - 1 são reflexões em torno da reta.

f x = 1 - 2 x 2 ,     x > 0

Passo 1

Usando a função f ( x ) devemos encontrar a função inversa f - 1 e plotar ambas em um mesmo gráfico juntamente com a função y = x para verificar se existe simetria. Sendo assim, para encontrarmos uma expressão para f - 1 seguiremos os seguintes passos:

Passo 1: escrever y = f x .

Passo 2: Resolva essa equação para x em termos de y , ou seja, trocando x por y e y por x (se possível).

Passo 3: a nossa função inversa vai ser dada isolando o nosso novo y .

Passo 2

Como a função já está no formato y = f ( x ) , vamos direto para o passo 2. Assim, teremos

y = 1 - 2 x 2 → x = 1 - 2 y 2

x - 1 = 2 y 2 → y 2 ⋅ 1 - x = 2

y 2 = 2 1 - x

y = 2 1 - x  

Passo 3

Plotando todos os gráficos juntos teremos

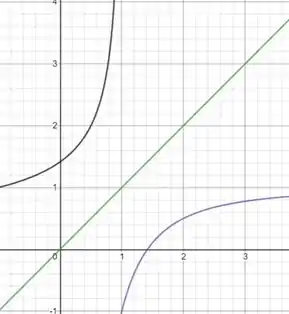
Podemos verificar que acertamos pois, obtemos funções simétricas em relação a reta y = x .

Resposta

f - 1 ( x ) = 2 1 - x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Complete as identidades usando o método do triângulo (Figura 0.4 . 15 ) cos ⁡ arctg ⁡ x =? tg ⁡ arccos ⁡ x =? sen ⁡ arcsec ⁡ x =? cotg ⁡ arcsec ⁡ x =?
Enfocando conceitosA função arccotg ⁡ x é definida como sendo a inversa da função cotangente restrita: cotg ⁡ x , 0xπ E a função arccossec ⁡ x é definida como sendo a inversa da função cossecante rest
Use um recurso computacional para aproximar a solução da equação. Quando forem usados radianos, expresse sua resposta com quatro casas decimais; quando forem usados graus, expresse-a até o décimo de g
Enfocando conceitosA função arccotg ⁡ x é definida como sendo a inversa da função cotangente restrita: cotg ⁡ x , 0xπ E a função arccossec ⁡ x é definida como sendo a inversa da função cossecante rest
Use um recurso computacional para aproximar a solução da equação. Quando forem usados radianos, expresse sua resposta com quatro casas decimais; quando forem usados graus, expresse-a até o décimo de g