Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 38
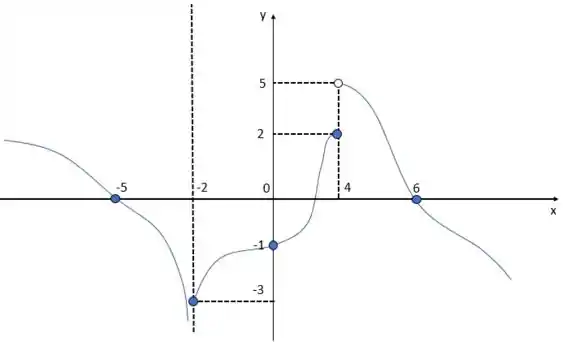
Faça um esboço do gráfico da função f que satisfaça as condições dadas:
Passo 1
Para esboçar esse gráfico, tenha em mente que a resposta pode ser bem subjetiva. Existem várias e várias funções que satisfazem a essas condições dadas, mas vamos esboçar aqui uma função que seja simples, ok?
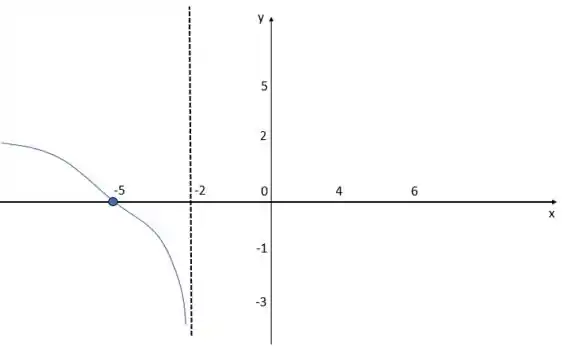
O primeiro passo é ver que, como a função é contínua em , o limite dessa função para qualquer valor nesse intervalo é exatamente o valor da função nesse ponto.
Assim, sabemos que e próximo de 2 tende ao infinito negativo.
Passo 2
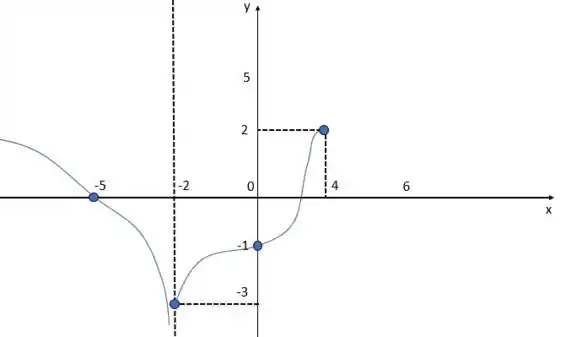
Agora, sabemos que a função é contínua no intervalo e, da mesma forma, qualquer limite pra valores dentro desse intervalo são exatamente a f no ponto.
Logo, , pois f é contínua pela esquerda de 4.
Passo 3
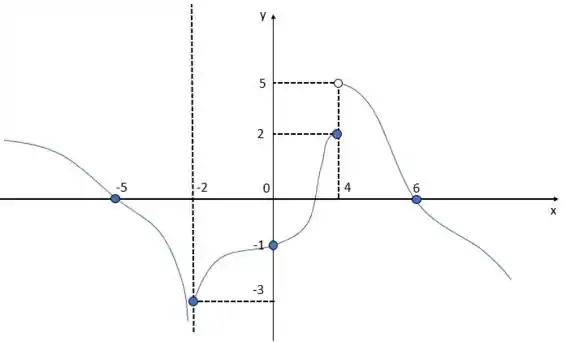
Por fim, sabemos que a função é contínua no intervalo e, da mesma forma, o valor do limite pra qualquer número que esteja nesse intervalo é exatamente a f no ponto. Assim, e próximo de 4 pela direita a função tende a 5, por conta do limite.
Passo 4
Note que se a função vai sempre decrescer depois do 5, ou se faz ondulações, ou se sempre cresce depois de um determinado número é uma subjetividade inerente desse tipo de questão e todas as alternativas que façam as ressalvas dos limites e da continuidade estão certas e são válidas.
Resposta
