Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 37
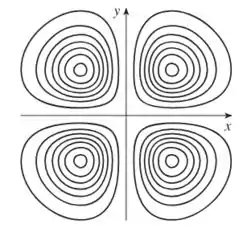
Faça um esboço de um mapa de contorno para a função cujo gráfico é mostrado.
Passo 1
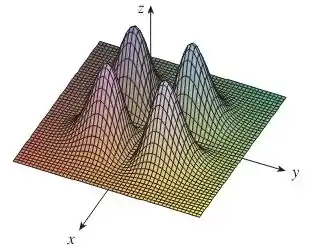
Eaee, belezinha?? Bom... queremos fazer um esboço com as curvas de nível da seguinte figura:
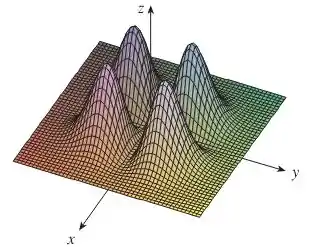
Para isso, temos que analisar o que acontece quando variamos :
- As curvas de nível mais próximas entre si indicam uma mudança mais rápida na altura ;
- As curvas mais espaçadas indicam uma mudança mais lenta em .
Agora bora aplicar!! 😉
Passo 2
Perceba que temos picos em cada quadrante de .
Perceba que, quanto maior , mais próximas serão as curvas delas mesmas. E o contrário acontece para valores menores de .
Com base nessas informações, temos as seguintes curvas de nível:
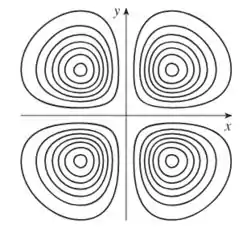
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 61-64, encontre uma equação para a superfície de nível da função que passa pelo ponto dado. g x ,y ,z = x - y + z 2 x + y - z ,1 ,0 ,- 2
Nos Exercícios 53-60, esboce uma superfície de nível típica para a função. f x ,y ,z = z - x 2 - y 2
Nos Exercícios 53-60, esboce uma superfície de nível típica para a função. f x ,y ,z = l n l nx 2 + y 2 + z 2
Nos Exercícios 53-60, esboce uma superfície de nível típica para a função. f x ,y ,z = z
Nos Exercícios 61-64, encontre uma equação para a superfície de nível da função que passa pelo ponto dado. f x ,y ,z = x - y - l n l nz,3 ,- 1 ,1