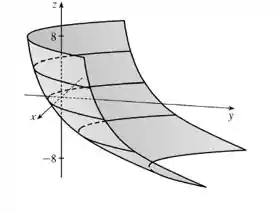
Um mapa de contorno de uma função é mostrado. Use-o para fazer um esboço aproximado do gráfico de f.
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade. Vem comigo que é só sucesso.
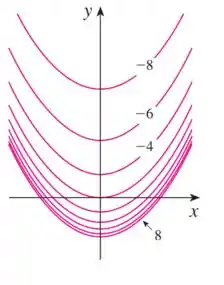
A gente tem o gráfico a seguir:
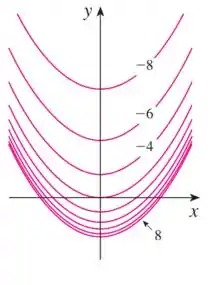
E ele representa a curva de nível de uma curva do tipo:
O que devemos ter em mente aqui é que uma curva de nível é a planificação da curva tridimensional, onde o eixo está em direção a tela.
Então devemos ‘puxar’ a figura planificada em nossa direção para que possamos ter noção de como é a curva tridimensional.
Devemos notar também que a orientação da nossa figura terá a seguinte forma:
z
x
y
Então devemos notar que a parábola está para o nosso rosto com o seu vértice.
Passo 2
Dá pra perceber que o gráfico cresce à medida que se anda pelo eixo no seu sentido contrário.
O crescimento vai se tornando mais rápido, já que as curvas vão se estreitando.
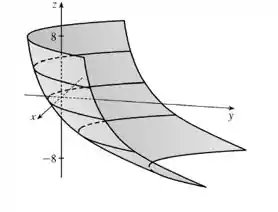
Resposta