Nos Exercícios 53-60, esboce uma superfície de nível típica para a função.
Passo 1
Oi galerinha, tudo bem com vocês? Vamos fazer esse exercício juntos?! Então, vem comigo!
No plano, os pontos onde uma função de duas variáveis independentes tem um valor constante formam uma curva no domínio da função. No espaço, os pontos onde uma função de três variáveis independentes tem um valor constante formam uma superfície no domínio da função.
O conjunto de pontos no espaço onde uma função de três variáveis independentes tem um valor constante é chamado superfície de nível de .
No nosso exercício, temos a seguinte equação:
O valor de é a distância entre a origem e o ponto .
É muito difícil visualizar uma função de três variáveis por seu gráfico, uma vez que estaríamos em um espaço de quatro dimensões. Entretanto, conseguimos uma ideia de desenhando suas superfícies de nível, que são as superfícies com equação , onde é uma constante. Se um ponto se move ao longo de uma superfície de nível, o valor de permanece fixo.
Passo 2
Então, se considerarmos que , temos:
Se aplicarmos exponencial de ambos os lados:
Temos a equação:
Gerando a Figura de uma esfera:
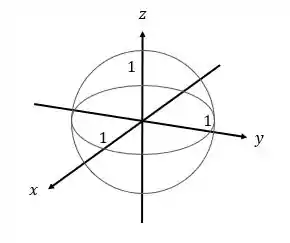
Tchau galerinha!
Resposta
Resposta no Passo 2.