Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção e então aplicando as transformações apropriadas.
Passo 1
Eaee, belezinha??? Bom... a quest��o nos fala para fazer o gráfico da seguinte função:
Mas para isso, devemos utilizar as funções básicas dadas na seção .
Assim, vamos comparando com essas funções e assim vamos construindo o gráfico, certinho??
Se liga... uma das funções parecidas é:
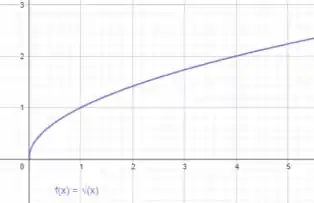
Então vamos analisar qual a diferença entre as duas funções para poder definir como será o gráfico, beleza?
Vamos usar as operações gráficas, aqui vale lembrar que:
Quando somamos um valor ao da função, andamos com ela pra esquerda.Quando subtraímos um valor ao da função, andamos com ela pra direita.Quando somamos um valor a toda a função, andamos com ela pra cima.E por fim, quando subtraímos um valor a toda a função, andamos com ela pra baixo.
Além disso, podemos perceber que a nossa função se trata de um módulo. Quando formos aplicar o módulo a nossa função, vamos transformar todos os valores negativos de em positivos, afinal é isso que a função módulo faz, ela faz com que tudo que é negativo retorne um valor positivo.
Então bora lá!! 😉
Passo 2
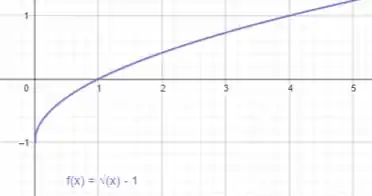
Vamos começar primeiro fazendo e comparar com .
Perceba que a única diferença é aquele , o que significa o deslocamento da curva em uma unidade para baixo no gráfico de , afinal estamos subtraindo uma unidade a toda a nossa função.
Passo 3
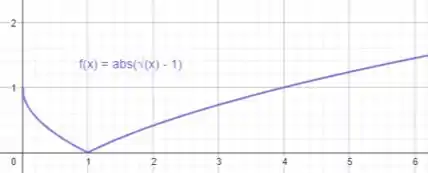
Agora vamos comparar e com .
Perceba que a única diferença é aquele módulo, o que significa que devemos rebater o lado negativo de para o lado positivo.
Tudo que é negativo fica positivo!
Com isso, temos o gráfico de :
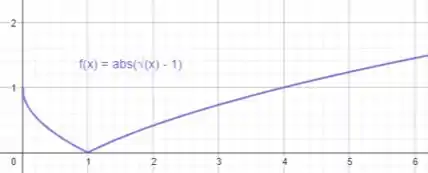
Entendeu direitinho?? Responde aee 😉
Resposta