- Faça o gráfico da curva Em quantos pontos da curva tem-se a impressão de que a curvatura possui um máximo local ou absoluto?
- Use um SCA para determinar e fazer o gráfico da função curvatura. Esse gráfico confirma sua conclusão na parte (a)?
Passo 1
Fala ai galerinha. Bora resolver uma questãozinha de gráficos?
Nesta questão temo com objetivo analiar a curva e verificar a quantidade de pontos da curva que possui um máximo ocal ou absoluto. O que podemos fazer para resolver?
Vamos calcular a derivadas de , calcular também a curvatura , identificar so pontos de máximo local ou aboluto da curvaduta e por fim traçar e analisar visualmente a curvatura por meio de um software
Bora!
Passo 2
Primeira derivada :
Segunda derivada :
Passo 3
Calcular a curvatura
Calculando o produto vetorial
Passo 4
Calculando o determinante:
Simplificando cada componente:
Passo 5
Calculando a magnitude
Para identificar os pontos onde a curvatura tem máximos locais ou absolutos, precisamos encontrar os pontos onde a derivada da curvatura em relação a é zero e verificar se esses pontos correspondem a máximos.
Passo 6
Através do gráfico podemos identificar pontos onde a curvatuda tem méximo locais ou absolutos.
a) Usando um software para construir o gráfico temos em cada eixo.
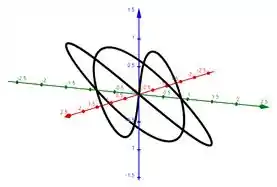
Gráfico de , em função de
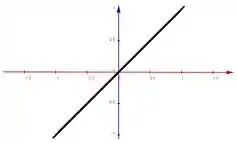
Gráfico de , em função de
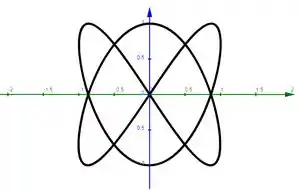
Analisando o gráfico aparentemente temos 3 máximos na função.
Passo 7
b)
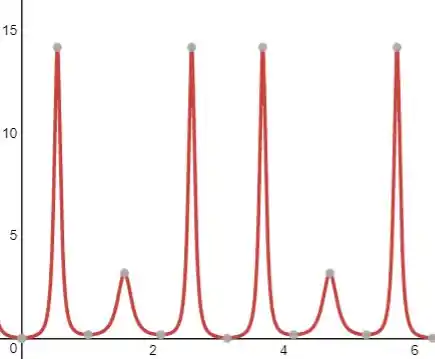
Ao observar o gráfico da função curvatura , podemos confirmar se nossa análise está correta. Se o gráfico mostrar picos em locais esperados, como múltiplos de , isso confirma nossa análise inicial.
Esse procedimento utilizando um SCA (SymPy) para calcular e plotar a curvatura fornece uma visualização clara e confirma a análise teórica da parte (a).
Resposta
- 3
- Sim.