Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 30
Encontre as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.
Passo 1
A equação vetorial da curva é
E temos o ponto:
E precisamos encontrar as equações paramétricas da reta tangente a está curva, no ponto que nos foi indicado.
Precisamos descobrir o valor do parâmetro no ponto considerado. Para isso, vamos igualar as componentes às coordenadas do ponto em questão.
Do sistema de equações acima, obtemos
sendo um inteiro. Para cálculos posteriores podemos tomar . Após isso, iremos então utilizar esse ponto para encontrar o valor do coeficiente angular da reta tangente. Ele é dado por:
Passo 2
A derivada da função vetorial é dada por
Portanto, o vetor tangente no ponto especificado, ou seja, para , é:
Passo 3
Com a inclinação linear, podemos montar a equação geral da reta parametrizada:
O ponto nos foi dado:
Então temos que a equação é:
E para que tenhamos a equação paramétrica a gente coloca cada coordenada isolada com o seu parâmetro :
Passo 4
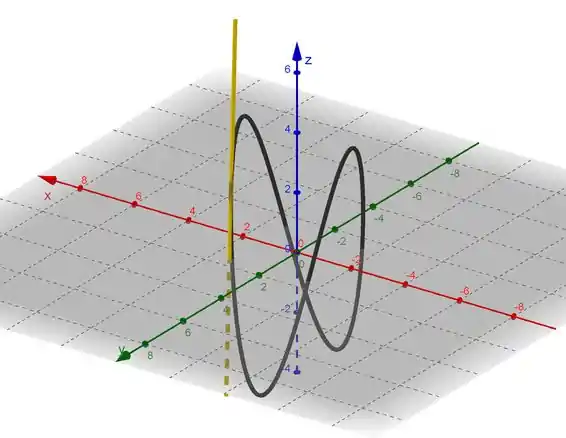
Com base nas equações paramétricas da curva e da reta é possível traçar os gráficos de ambas numa mesma tela utilizando softwares como mostrado abaixo:
