Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 6
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma arbitrária qualquer contínua em .
6-
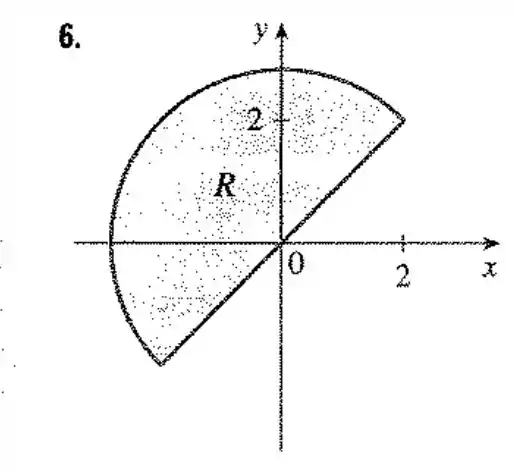
Passo 1
Essa questão é mais legal, é mais fácil encontrar os parâmetros para esse problema em coordenadas polares porém precisamos saber ver qual o valor de e para essa figura.
O valor de é o valor da hipotenusa formada pelo triângulo retângulo com catetos e visto abaixo.
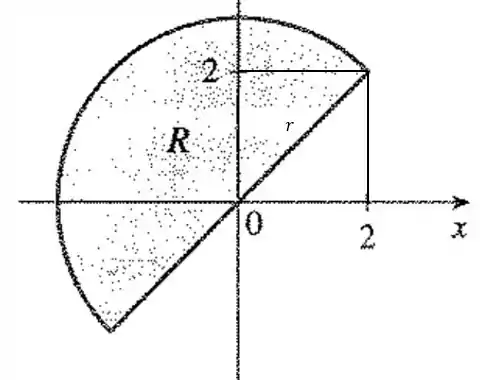
Dessa forma por Pitágoras temos:
Então vai de até .
Passo 2
Como a reta inclinada passa por e por então podemos ver por que essa reta é igual a e essa reta por ter coeficiente angular igual a nos diz que ela faz uma ângulo com a horizontal igual a e por ela ser um semi círculo nos diz que ela vai de até , logo a integral iterada para a função seria igual a:
Essa visão você precisa realmente ter sobre coordenadas polares, o quanto que se varia para completar área e o percorrimento de indo do começo até o final no sentido anti-horário