Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 17.1 - Ex. 15

Faça o gráfico das duas soluções básicas da equação diferencial e de várias outras soluções. Que aspecto as soluções têm em comum?

d 2 y d x 2 + 2 d y d x + 2 y = 0

Passo 1

Galerinha, se tivermos uma equação diferencial de segunda ordem da forma

a y ' ' + b y ' + c y = 0

uma solução pode ser encontrada através das raízes da equação auxiliar (ou equação característica) que é escrita como

a r 2 + b r + c = 0

As raízes dessa equação vão ajudar a dar forma a solução da equação diferencial. A tabela abaixo nos dá as possibilidades de raízes e suas respectivas formas de soluções gerais.

Vamos escrever a equação característica da nossa questão:

r 2 + 2 r + 2 = 0

Usando a fórmula de Bhaskara para achar as raízes:

r = - b ± b 2 - 4 a c 2 a

r 1 = - 2 + 4 - 4 1 2 2 = - 1 + i

r 1 = - 2 - 4 - 4 1 2 2 = - 1 - i

Passo 2

Encontramos no passo anterior as raízes complexas! Portanto, a solução geral pode ser escrita da seguinte forma:

y = e - 1 ( c 1 cos ⁡ x + c 2 sen ⁡ x )

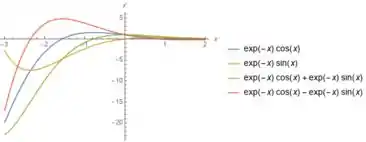
Abaixo, nós temos os gráficos das mais diversas soluções que a equação diferencial tem.

Resposta

A solução geral da equação é:

y = e - 1 ( c 1 cos ⁡ x + c 2 sen ⁡ x )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema de valor limite, se possível. 4 y ' ' - 4 y ' + y = 0 , y 0 = 4 , y 2 = 0
Resolva o problema de valor limite, se possível. y ' ' = y ' ,y 0 = 1 , y 1 = 2
Resolva o problema de valor limite, se possível. y ' ' + 4 y ' + 20 y = 0 , y 0 = 1 , y π = e - 2 π
Encontre uma equação diferencial cuja solução geral é y = c 1 e - t / 2 + c 2 e - 2 t .
Em cada um dos problemas de 1 a 8, encontre a solução geral da equação diferencial dada. 4 ⋅ y ' ' - 9 ⋅ y = 0