Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 67
- Faça o gráfico da função
- Qual a aparência do período dessa função?
- Confirme sua conclusão sobre o item (b) algebricamente.
Passo 1
E aí, pessoas! Bora pra mais uma?
Na letra (a) ele quer que você apenas monte o gráfico, sem mistérios.
Na letra (b) você vai dizer qual é o provável período da função.
E na letra (c) você vai mostrar com continhas a sua conclusão.
Bora lá?
Passo 2
(a)
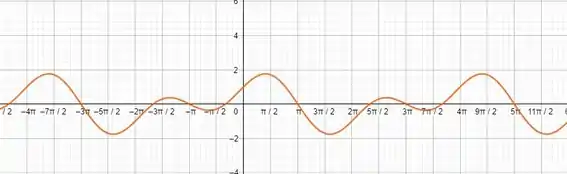
A letra (a) é a mais direta. O gráfico da função é meio doidão. Fica assim:
Passo 3
(b)
Seguinte: vamos olhar bem pra carinha do gráfico. Ela parece ser totalmente irregular, né? Mas não é, ela tem uma lógica. Repara comigo: ela começa a subir e a descer normalmente e, de repente, ela dá um tremelique doido e aí volta a subir e a descer normalmente, certo?
O período de uma função é a distância, no eixo de um ponto do gráfico até o próximo ponto “equivalente” a ele.
Vamos escolher aquele ponto que cruza com o eixo y, ok? Tá vendo que antes dele a função deu um tremelique e subiu? Vamos procurar a próxima vez que vai ter esse mesmo padrão (tremelicar e subir). Ali no aconteceu isso e ele parece ser o correspondente do que a gente olhou inicialmente (é como se você colocasse uma régua na horizontal e visse que os dois pontos são passados por essa régua).
Então, o período é, aproximadamente, .
Passo 4
(c)
Agora vamos fazer as continhas:
a função dada foi . Vamos jogar ali dentro.
Bom, o é o mesmo ponto que uma volta anterior no Círculo Trigonométrico, que é a mesma coisa que , uma volta antes. Então:
, que é a nossa função original!
Lembra que um período é onde tem os primeiros pontos correspondentes? Ali, te provei que , logo, se e são correspondentes, ou seja, é o período.
Resposta
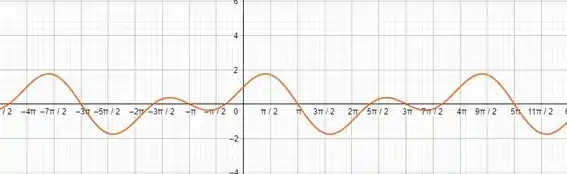
(b)