Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 58
Faça o gráfico da função . Qual o período da função?
Passo 1
Olá, pessoas cheirosas! Vamos lembrar de uma coisa: o período de uma função é a distância (no eixo ) de um pico (também chamado de “crista”) de uma “onda” até a outra. Essa “onda” aqui pode ser o seno ou o cosseno, beleza? Bora começar.
Passo 2
Agora a resposta é na lata!
Saca só o gráfico da função:
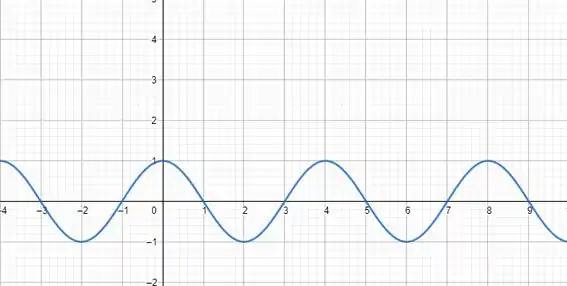
Qual é a distância entre uma crista e outra? É . É só olhar que, quando , tem uma crista e a próxima é quando . Simples assim!
Resposta
4
Exercícios de Livros Relacionados
Ache a t g ( θ ) se θ for o ângulo de inclinação entre as retas com as inclinações 1 e 1 4 .
Ache, com aproximação de 1 grau, a medida do ângulo entre as retas com as inclinações - 3 e 2 .
Ache a t g ( θ ) se θ for o ângulo de inclinação entre as retas com as inclinações - 1 2 e 2 3 .
Para que valores de t em [ 0 ,2 π ] temos t g ( t ) indefinida.
Para que valores de t em [ 0 , 2π ) temos s e c ( t ) indefinida.