Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 59
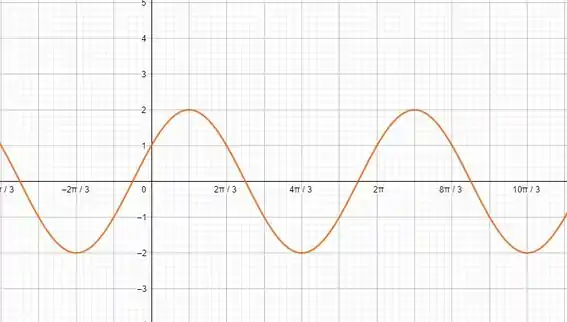
Faça o gráfico de ).
Passo 1
Olá, gente! Vamos lembrar uma coisa antes de começarmos a questão:
Se você quer (em n unidades):
Subir um gráfico: basta somar n unidades LONGE do ;
Descer um gráfico: basta subtrair n unidades LONGE do ;
Mover um gráfico para a direita: basta subtrair n unidades PERTO do (do ladinho dele);
Mover um gráfico para a esquerda: basta somar n unidades PERTO do (do ladinho dele);
Alongar verticalmente um gráfico: basta multiplicar por n unidades a equação toda;
Comprimir verticalmente um gráfico: basta dividir por n unidades a equação toda;
Comprimir horizontalmente um gráfico: basta multiplicar o por n;
Alongar horizontalmente um gráfico: basta dividir o por n;
Refletir um gráfico em torno do eixo y: basta substituir por ;
Refletir um gráfico em torno do eixo x: basta multiplicar a função toda por -1.
Vamos?
Passo 2
Para montar o gráfico do zero, nós temos que pegar um gráfico bem parecido com esse (no caso, ) e fazer algumas daquelas modificações que eu falei no PASSO 1 pra chegarmos em ). Ok?
Esse é o gráfico de :
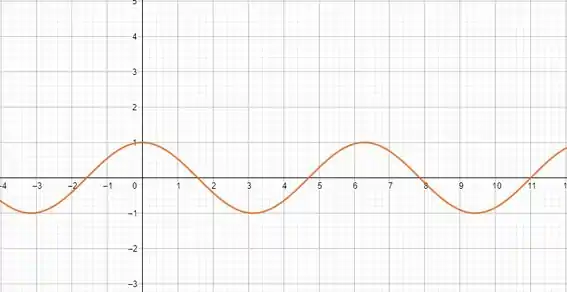
Partindo de , vamos:
- Multiplicar a função toda por 2;
- Subtrair dali pertinho do , dentro do cosseno.
Quais os efeitos que esses passos dão, no final das contas?
- Alongamento vertical de um fator de 2 unidades;
- Mover o gráfico em unidades para a direita.
Vai ficar assim:
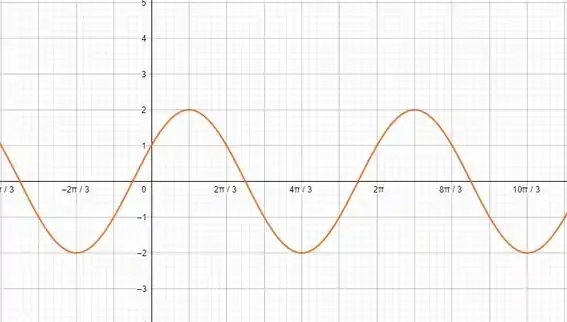
Sacou?
Resposta
