Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 88
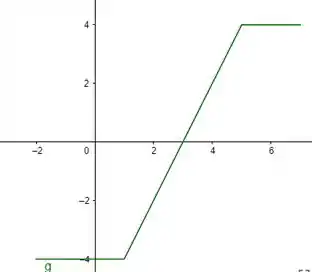
Faça o gráfico da função abaixo, localizando seus valores extremos e onde ocorrem.
Passo 1
A função é linear, portanto podemos construir a função calculando ponto a ponto.
Depois disso, é só caracterizar os pontos de máximo e de mínimo no intervalo
Passo 2
Esquematizando todos os pontos em uma tabela, temos:
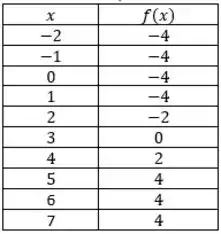
Passo 3
Desenhando o gráfico, teremos:
Resposta
Exercícios de Livros Relacionados
f x = 7 + x 11 - 3 x 1 / 3 possui um valor mínimo absoluto? Um máximo absoluto? Em caso afirmativo, determine-os ou justifique sua ausência. Apresente todos os pontos críticos de f .
f x = x 3 + 2 x + t g x possui algum valor mínimo ou máximo local? Justifique sua resposta.
g ( x ) = c o s s e c x + 2 c o t g x possui valores máximos locais? Justifique sua resposta.
f ( x ) = 2 e x / ( 1 + x ² ) ² possui um valor mínimo absoluto? E um máximo absoluto? Em caso afirmativo, calcule-os; do contrário, explique por que eles não existem. Liste todos os pontos críticos d
g ( x ) = e x - x possui um valor mínimo absoluto? E um máximo absoluto? Em caso afirmativo, calcule-os; do contrário, explique por que eles não existem. Liste todos os pontos críticos de g .