Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.1 - Ex. 6

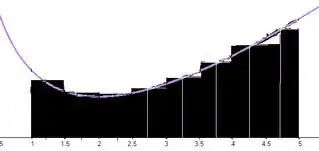
  1. Faça o gráfico da função

    2. f x + x - 2 ln ⁡ x   ,   1 ≤ x ≤ 5  

  2. Estime a área sob o gráfico de f usando quatro retângulos aproximastes e tomando como pontos amostrais ( i ) as extremidades direitas e ( i i ) os pontos médios. Então, aperfeiçoe sua estimativa utilizando seis retângulos aproximantes. Esboce a curva e os retângulos aproximantes.
  3. Aperfeiçoe suas estimativas da parte ( b ) usando oito retângulos.

Passo 1

Vamos fazer o gráfico da função primeiro, beleza?

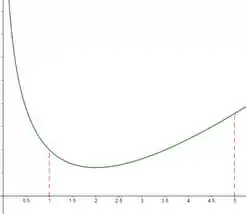
Vamos usar os gráficos para estimar os valores que vamos precisar, certo?

Passo 2

Agora, precisamos estimar a área usando quatro retângulos. Perceba que da nossa fórmula a = 1 e b = 5. Além disso,

Δ x = 5 - 1 n

Como precisamos de 4 retângulos, ou seja, quando n = 4 . Daí, Δ x = 5 - 1 4 = 1

Temos os intervalos:

1,2 ; 2,3 ; 3,4 ; 4,5 .  

Passo 3

Vamos resolver o item i) da letra b). Isto é usar como pontos amostrais as extremidades direitas. Partxiiu!

Nossos pontos a ser usados são x i = 1 + i   Δ x   Ou seja,     x 1 = 2 ;     x 2 = 3   ; x 3 = 4 ; x 4 = 5   .

Daí, substituindo na fórmula,

A s =   ∑ i = 1 n   f x i Δ x   = f x 1 + f x 2 + ⋯ + f x 4   =   f 1 + f 3 + ⋯ + f 5  

Olhando no gráfico,

f 1 + f 3 + ⋯ + f 5 = 0,61 + 0,8 + 1,23 + 1,78 = 4,42

Que correspondem aos retângulos

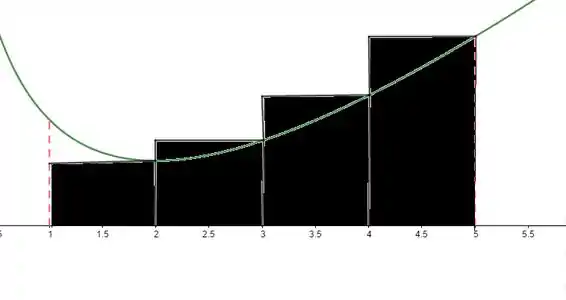
Passo 4

Agora, vamos usar os pontos médios. Ou seja, x 1 = 1,5 ; x 2 = 2,5 ; x 3 = 3,5 ; x 4 = 4,5

Desenhando os retângulos, temos :

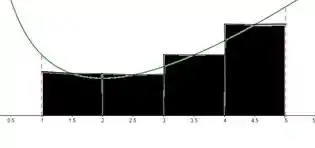
Substituindo na fórmula,

A i =   ∑ i = 1 n   f x i Δ x   = f x 1 + f x 2 + ⋯ + f x 4   =   f 1,5 + f 2,5 + ⋯ + f 4,5

Olhando no gráfico, temos

=   f 1,5 + f 2,5 + ⋯ + f 4,5 = 0 ,   70 + 0,66 + 0,99 + 1,49 = 3,84

Passo 5

Agora vamos usar 8 retângulos. Daí,

Δ x = 5 - 1 8 = 1 2

Temos os intervalos:

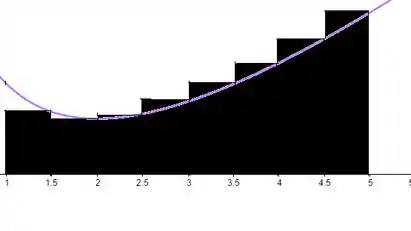
1 , 3 2   ; 3 2 , 4 2 ; 4 2 , 5 2 5 2 , 6 2 ; 6 2 , 7 2 ; 7 2 , 8 2 ; 8 2 , 9 2 ; 9 2 , 10 2 .  

Vamos usar como pontos amostrais as extremidades direitas. Partxiiu!

Nossos pontos a ser usados são x i = 1 + i   Δ x   Ou seja,     x 1 = 3 2 ;     x 2 = 2   ; x 3 = 5 2 ; x 4 = 3   ; x 5 = 7 2 ; x 6 = 4   ; x 7 = 9 2 ; x 8 = 5   . .

Daí, substituindo na fórmula,

A s =   ∑ i = 1 n   f x i Δ x   = f x 1 + f x 2 + ⋯ + f x 8   =   f 3 2 + f 2 + ⋯ + f 5  

Olhando no gráfico,

f 1 + f 3 + ⋯ + f 5 = 0,70 + 0,61 + 0,66 + 0,60 + 0,99 + 1,23 + 1,49 +   1,78 = 8,06

Que correspondem aos retângulos

Passo 6

Usando os pontos médios, ou seja, x 1 = 1,25   ; x 2 = 1,75   ; x 3 = 2,25   ; x 4 = 2,75   ; x 5 = 3,25   ; x 5 = 3,75   ; x 6 = 4,25   ; x 7 = 4,75

Substituindo na fórmula,

A i =   ∑ i = 1 n   f x i Δ x   = f x 1 + f x 2 + ⋯ + f x 4   =   f 1,25 + f 2,25 + ⋯ + f 4,75

Olhando no gráfico, temos

=   f 1,5 + f 2,5 + ⋯ + f 4,5 = 0 ,   80 + 0,63 + 0,63 + 0,73 + 0,89 + 1,11 + 1,35 + 1,63 = 7,14

Resposta

D e m o n s t r a ç ã o .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Estime a área sob o gráfico de f x = cos ⁡ x de x = 0 até x = π 2 usando quatro retângulos aproximantes e extremidades direitas. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativ
Expresse o limite como uma integral definida no intervalo. lim n → ∞ ⁡ ∑ i = 1 n cos ⁡ x i x i Δ x , [ π ,2 π ]
A velocidade de um corredor aumenta regularmente durante os três primeiros segundos de uma corrida. Sua velocidade em intervalos de meio segundo é dada em uma tabela. Ache as estimativas superior e in
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ 1 4 x 2 + 2 x - 5d x