Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 77

Faça o gráfico da função na janela , . Explique o que você vê. Como poderia alterar a fórmula para virar os arcos de cabeça para baixo?

Passo 1

Então, povo, no Passo 2 nós vamos montar o gráfico das funções e vamos concluir algo sobre ele, beleza? Bora lá.

Passo 2

Bom, galera, no intervalo que ele pediu, vai ficar assim:

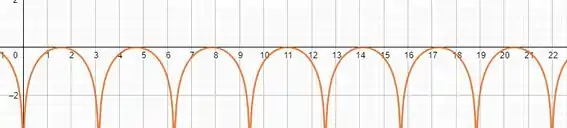
Com os ângulo no eixo x, fica assim:

O que podemos concluir? Podemos concluir que se trata de um gráfico com concavidades periódicas (ou seja, se repetem com uma frequência) voltadas para baixo e que, deem ela não está definida.

Como fazer os arcos virarem pra cima? Pra isso acontecer, temos que fazer o gráfico refletir em torno do eixo x e, pra isso, basta multiplicar a função toda por -1, ficando

Resposta

Podemos concluir que se trata de um gráfico com concavidades periódicas (ou seja, se repetem com uma frequência) voltadas para baixo e que, deem ela não está definida. Para fazer os arcos virarem para cima, basta multiplicar a função toda por -1, ficando

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.As curvas da família y = - 5 s e n ( A π x ) têm amplitude 5 e período 2 / A .

Combine a equação com seu gráfico na figura a seguir e determine as equações para asassíntotas verticais ehorizontais. (a) y = x 2 x 2 - x - 2 (b) y = x - 1 x 2 - x - 6 (c) y = 2 x 4 x 4 + 1 (d) y = 4

Encontre uma equação da forma y = k x 2 + b x + c cujo gráfico se adeque razoavelmente com o da figura abaixo. Confira seu trabalho com um recurso gráfico.

Encontre uma equação da forma y = D + A s e n ( B x ) ou y = D + A c o s ( B x ) para cada gráfico.