Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 22
Um fabricante de recipientes impermeabilizados de papelão para bebidas quer construí-los na forma de um paralelepípedo fechado com base quadrada e capacidade de 1/10 litro (100 cm3). Dê uma estimativa para as dimensões do recipiente que requer a menor quantidade de material para sua fabricação.
Passo 1
O recipiente que requer a menor quantidade de material é aquele com a menor área. E, como será um recipiente na forma de paralelepípedo com base quadrada, a área dele será a soma das áreas das laterais com as áreas da tampa e da base:
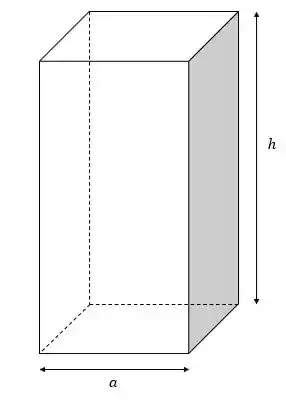
Como podemos ver, serão 4 áreas dos retângulos das laterais e duas áreas de quadrados, um da tampa e outro da base. Com isso, a área lateral:
Mas vamos achar uma relação entre e para ter algo mais concreto haha.
Passo 2
Queremos que o recipiente tenha de capacidade. O volume dele é dado pela multiplicação da área da base pela altura:
A base é um quadrado, como vimos na imagem anterior, assim:
Dessa forma, vamos substituir :
Assim, podemos substituir essa informação na equação para a área lateral:
Opa, então temos a área lateral em função do lado do quadrado da base, certo? Vamos jogar isso num gráfico, lembrando que só teremos valores positivos para , já que é uma medida de comprimento:
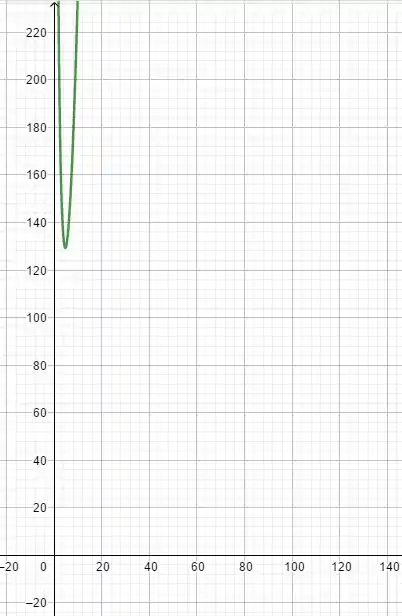
Como queremos a menor área lateral possível, vemos que o menor valor da função ocorre em aproximadamente quando . Então, esse será o valor do lado do quadrado da base.
A altura será dada pela relação que achamos ali em cima:
Prontinho!
Resposta
Base quadrada com lado e altura