Use o roteiro desta seção para esboçar a curva:
Passo 1
Eaeee, belezinha??? Bom... A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva da seguinte função:
Assim, precisamos encontrar o domínio da função, interseção com eixos, limites no infinito, intervalos de crescimento, pontos críticos, fazer um estuda da concavidade e qualquer outra consideração que ajude a entender bem o comportamento da função.
Eiiita, muita coisa né??? Então vamos com calma que vai dar certo!!!
😉
Passo 2
Nosso primeiro passo é calcular o domínio.
O domínio de uma função é o conjunto de todos os valores de entrada para os quais a função produz um resultado válido.
Sabendo disso, é importante observar as restrições que uma função pode ter.
No nosso caso, a questão já nos disse o domínio , que é o intervalo , portanto:
Passo 3
Agora precisamos achar os pontos de interceptação nos eixos.
Fazendo , temos o ponto de interceptação no eixo :
Que é a origem.
Agora, fazendo , temos:
É muito complicarmos para nós resolvermos analiticamente essa expressão.
No entanto, se fizermos através de um método numérico (pelo método de Newton-Raphson, por exemplo) chegaremos nos seguintes resultados:
Passo 4
A figura haverá simetria se a função for par ou ímpar.
Para isso vamos fazer :
Logo, vemos que a função é ímpar e há simetria a partir do zero.
Passo 5
As assíntotas verticais ocorrem quando o denominador da função se anula.
Nesse sentido, temos:
Assim, as assíntotas verticais estão em .
Não há assíntotas horizontais.
Passo 6
Encontrando os intervalos de crescimento e decrescimento, a gente deriva a função e verificamos se a derivada é positiva ou negativa em relação ao intervalo:
Analisando a derivada, observamos que:
Sendo assim, cresce em
e decresce em
e em
Passo 7
Como a função decresce depois cresce, e decrescente novamente, há um valor de máximo local em , e um de mínimo local em .
Passo 8
Achando concavidades e pontos de inflexão por meio da derivada segunda, temos:
,
e
Assim, a função tem concavidade para cima em , e concavidade para baixo em e um ponto de inflexão em onde a derivada troca o sinal.
Com base nessas informações, temos o seguinte gráfico:
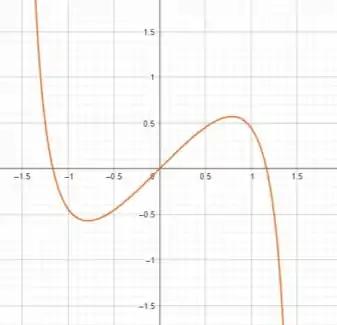
Resposta
Resposta nos passos