Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 66

Altura de um balão meteorológico: Observadores nas posições A e B distantes 2km um do outro medem simultaneamente o ângulo de elevação de um balão meteorológico como sendo de 40° e 70°, respectivamente. Se o balão está diretamente acima de um ponto no segmento da reta entre A e B , determine a altura do balão.

Passo 1

E aí, galera! Vou te mostrar como fica o esboço desse desenho:

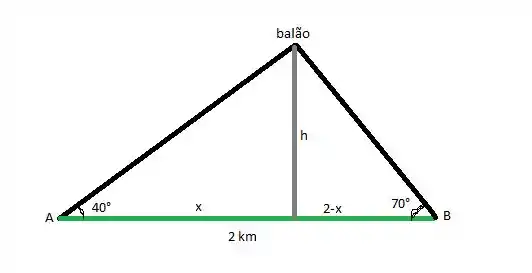
Pra esse problema, precisamos lembrar que:

tangente: t g x = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e

Aqui, nós vamos:

  1. Achar duas relações entre h e x;
  2. Isolar o x em uma relação;
  3. Jogar o x na segunda relação e achar h.

Beleza? Então partiu!

Passo 2

Nesse passo, vamos fazer o (1) daquele passo-a-passo ali em cima.

Olha bem pro desenho. Agora olha pro triângulo que tem o ângulo de 40°. Se eu quero uma relação que contenha x e h (que são catetos) e foi dado um ângulo, vamos usar a tangente desse ângulo!

t g x = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e → t g 40 = h x

Analogamente, vamos fazer a mesma coisa com o triângulo que tem o ângulo de 70°

t g x = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e → t g 70 = h 2 - x

Passo 3

Vamos fazer o (2) aqui. Vou usar essa equação t g 40 = h x pra isolar o x .

t g 40 = h x → x = h t g 40 (eu passei o x pro outro lado como multiplicação e o t g 40 como divisão)

Show? Bora pro Passo 3!

Passo 4

Vamos fazer o que está no (3) e jogar x = h t g 40 em t g 70 = h 2 - x e aí é só isolar o h e prontinho!

t g 70 = h 2 - x → t g 70 = h 2 - h t g 40 . Tirando o mmc ali em baixo: t g 70 = h 2 - h t g 40 → t g 70 = h 2 ⋅ t g 40 - h t g 40 . Pela propriedade de divisão de frações (repete a primeira e multiplica pelo inverso da segunda): t g 70 = h 2 ⋅ t g 40 - h t g 40 → t g 70 = h ⋅ t g 40 2 ⋅ t g 40 - h . Passando 2 ⋅ t g 40 - h como multiplicação para o outro lado:

t g 70 ⋅ ( 2 ⋅ t g 40 - h ) = h ⋅ t g 40 → 2 ⋅ t g 70 ⋅ t g 40 - h ⋅ t g 70 = h ⋅ t g 40 Ali eu fiz a distributiva e agora vamos isolar o h . Passando - h ⋅ t g 70 pro outro lado como adição:

h ⋅ t g 40 + h ⋅ t g 70 = 2 ⋅ t g 70 ⋅ t g 40 → h ⋅ ( t g 40 + t g 70 ) = 2 ⋅ t g 70 ⋅ t g 40 → h = 2 ⋅ t g 70 ⋅ t g 40 t g 40 + t g 70

Olhando na tabela trigonométrica:

t g 40 ≈ 0,84

t g 70 ≈ 2,75

Vamos jogar esses valores em h = 2 ⋅ t g 70 ⋅ t g 40 t g 40 + t g 70 e aí achar o h .

h = 2 ⋅ t g 70 ⋅ t g 40 t g 40 + t g 70 → h = 2 ⋅ 2,75 ⋅ 0,84 0,84 + 2,75 → h = 4,62 3,59 ≈ 1,28 k m

Resposta

1,28km

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a t g ( θ ) se θ for o ângulo de inclinação entre as retas com as inclinações 1 2 e - 3 4 .
Ache, com aproximação de 1 grau, as medidas dos ângulos internos do triângulo com vértices (1, 0), (-3, 2) e (2, 3).
Ache, com aproximação de 1 grau, as medidas dos ângulos internos do triângulo formado pelas retas que têm equação 2 x + y - 6 = 0 , 3 x - y - 4 = 0 e 3 x + 4 y + 8 = 0 .
55. Fórmula para soma das tangentes A fórmula padrão para a tangente da soma de dois ângulos é tg ⁡ ( A + B ) = tg ⁡ A + tg ⁡ B 1 - tg ⁡ A tg ⁡ B Deduza a fórmula.
56. (Continuação do Exercício 55.) Deduza a fórmula para tg ⁡ ( A - B ) .