Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 57
Faça o gráfico da função . Qual o período da função?
Passo 1
Olá, pessoas cheirosas! Vamos lembrar de uma coisa: o período de uma função é a distância (no eixo ) de um pico (também chamado de “crista”) de uma “onda” até a outra. Essa “onda” aqui pode ser o seno ou o cosseno, beleza? Bora começar.
Passo 2
Agora a resposta é na lata!
Saca só o gráfico da função:
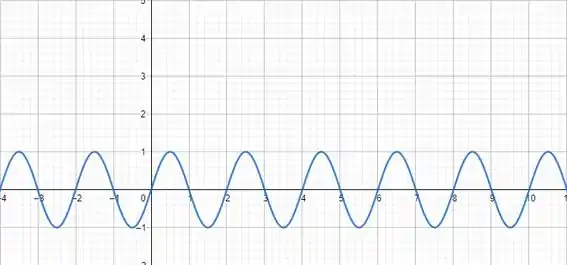
Aqui, a gente não consegue ver de cara qual que é o valor de nas cristas, mas não tem problema! Sabe por quê? Porque o período pode ser medido em outras partes da onda. Basta que os dois pontos tenham a mesma característica, o que quer dizer que, se você pegar um ponto que tá no meio da subida da onda, o outro ponto pra calcular o período vai estar na metade da próxima subida da onda. E é esse ponto que a gente vai escolher aqui. No, a onda tá na metade da subida. Agora é só achar o próximo.
Qual é a distância entre uma crista e outra? É . É só olhar que é o ponto da função mais próximo do que tem a característica de estar na metade da subida.