Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 76
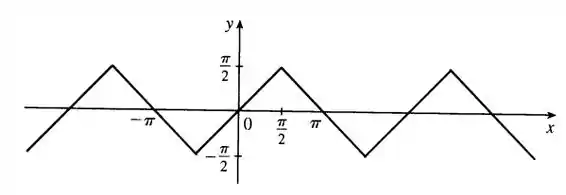
a) Faça o gráfico da função
E explique sua aparência
b) Faça o gráfico da função
Como você pode explicar a aparência desse gráfico?
Passo 1
Fala aí, pessoal! 😬
Nesse problema queremos obter o gráfico das funções a) e b) .
Parece complicado, né? 👀
Para esboçar esses gráficos temos que lembrar de algumas propriedades de funções trigonométricas inversas.
Bora lá! 😁
Passo 2
Primeiramente, para esboçar o gráfico da função temos que perceber o seguinte:
A função resulta no seno do ângulo cujo seno é ...
Ou seja, é a mesma coisa de falar “se o carro é azul, qual cor que o carro é pintado?”
Porem tem um pequeno problema... o seno varia de a , portanto o gráfico da função será obtida como
Esboçando o gráfico, ficamos com
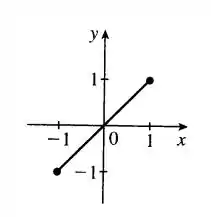
Tranquilo até aqui? 😉
Passo 3
Para o item b), temos .
O conceito inicial aqui é a mesma coisa do item anterior
Porém agora nosso gráfico não é mais limitado no intervalo .
Como o seno assume seus valores extremos em múltiplos de , a cada um desses múltiplos, a função será invertida.
Esboçando o gráfico, ficamos com
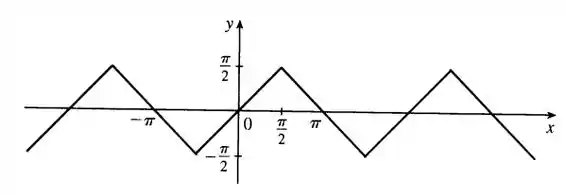
Legal, né? O que achou? Responde Aí! 😉
Resposta
a)
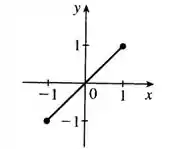
b)
