Fazer o gráfico da função
Depois, verificar se ela possui um mínimo absoluto.
Passo 1
É preciso saber o domínio da função. Como o logaritmando deve ser positivo:
Passo 2
Encontrar a primeira derivada da função:
Passo 3
Encontrar a segunda derivada da função:
Passo 4
Encontrar as raízes da função e de suas duas primeiras derivadas:
Passo 5
Fazer o estudo de sinais da função e de suas duas primeiras derivadas:
Passo 6
É preciso analisar se existem assíntotas verticais. Para isso, fazemos:
Obtemos uma indeterminação do tipo , então aplicaremos L’Hôpital:
Logo, não há assítota vertical.
Passo 7
É preciso analisar se existem assíntotas horizontais ou inclinadas. Para isso, fazemos:
Portanto, não existe assíntota horizontal.
Passo 8
Para facilitar o esboço, encontramos pontos notáveis na função:
Passo 9
Substituímos a raiz da primeira derivada na segunda derivada pra saber se é um ponto de máximo, de mínimo ou de inflexão:
Portanto, é um ponto de mínimo local. Porém, como é menor que os extremos da função, é um mínimo absoluto.
Resposta
Mínimo absoluto:
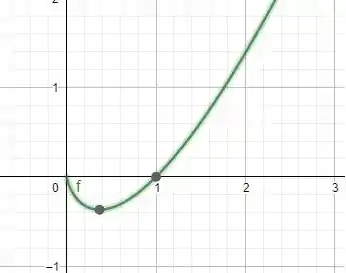 Esboço:
Esboço: