Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 75
Faça o gráfico das funções (quantas você puder) juntas para . O que ocorre? Explique.
Passo 1
Então, povo, no Passo 2 nós vamos montar o gráfico das funções e vamos concluir algo sobre ele, beleza? Bora lá.
Passo 2
Bom, galera, vai ficar assim:
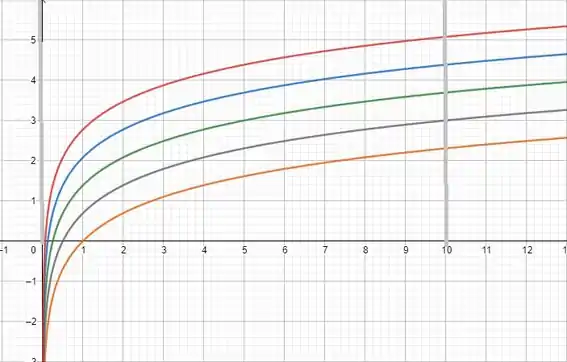
As barrinhas cinza estão delimitando o intervalo que foi pedido.
A cor laranja é a , a roxa é a e assim por diante.
Repare que elas estão se comprimindo horizontalmente cada vez mais e essa compressão tá sendo igual pra cada uma, porque elas estão com um espaçamento igual entre elas.
Como justificar isso?
Lembra que, quando tem , se você multiplicar coladinho ali perto do , a função sofre uma compressão horizontal? Foi isso que aconteceu. Mas qual o fator de compressão, ou seja, qual o número que entra multiplicando ali dentro? Se você olhar pra e pra , vai ver que o que mudou foi o 2 multiplicando ali dentro, né? E pra e ? Também multiplicou por 2 ali dentro. Ou seja, o fator de compressão pra cada uma em relação à anterior é de 2.
Resposta
Ocorre uma compressão horizontal por um fator de 2.