Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.3 - Ex. 50

Faça com que R seja uma região que fica entre as curvas:

y = x m ,     y = x n ,     0 ≤ x ≤ 1

Onde m e n são inteiros com 0 ≤ n < m .

a) Esboce a região R .

b) Encontre as coordenadas do centróide de R .

c) Tente encontrar valores de m e n de tal forma que o centróide fique fora de R .

Passo 1

Bom, vamos começar o exercício pela letra a). Se fizermos com que o intervalo de análise seja 0 ≤ x ≤ 1 , do enunciado temos que n < m , então como estamos nesse intervalo em específico, teremos x n > x m . O gráfico dessa região é mostrado a seguir:

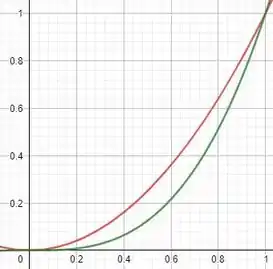
Passo 2

Agora vamos para a letra b). Usando a fórmula 9 fornecida nessa seção do livro, temos:

A = ∫ 0 1 x n - x m   d x = 1 n + 1 - 1 m + 1

Tirando o mínimo múltiplo comum entre as duas frações, podemos reescrever:

A = m - n ( n + 1 ) ( m + 1 )

Agora podemos calcular a posição do centróide, começando por x - :

x - = ( n + 1 ) ( m + 1 ) m - n ∫ 0 1 x x n - x m   d x = ( n + 1 ) ( m + 1 ) m - n ∫ 0 1 x n + 1 - x m + 1   d x

Aplicando novamente a fórmula 9, temos:

x - = n + 1 m + 1 m - n 1 n + 2 - 1 m + 2

x - = ( n + 1 ) ( m + 1 ) ( n + 2 ) ( m + 2 )

Agora para y - :

y - = ( n + 1 ) ( m + 1 ) m - n ∫ 0 1 1 2 x n 2 - x m 2   d x = ( n + 1 ) ( m + 1 ) 2 ( m - n ) ∫ 0 1 x 2 n - x 2 m   d x

Aplicando novamente a fórmula 9, temos:

y - = n + 1 m + 1 2 ( m - n ) 1 2 n + 1 - 1 2 m + 1

y - = ( n + 1 ) ( m + 1 ) ( 2 n + 1 ) ( 2 m + 1 )

Passo 3

Agora para a letra c), vamos chutar dois valores para n e m , fazendo n = 3 e m = 4 e substituindo nas equações encontradas no passo 2, temos:

x - , y - = 4.5 5.6 ; 4.5 7.9 → x - , y - = 2 3 ; 20 63

Esse centróide fica fora de R , já que:

2 3 3 = 8 27 < 20 63

Resposta

x - = ( n + 1 ) ( m + 1 ) ( n + 2 ) ( m + 2 )

y - = ( n + 1 ) ( m + 1 ) ( 2 n + 1 ) ( 2 m + 1 )

n = 3 ; m = 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44- Deduza a equação do volume de uma esfera de raio r usando o método da casca.
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 28 – A – O eixo x.
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 27 – C – A reta y = 8 5 .
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 27 – D – A reta y = - 2 5 .
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B