A luz entra pelo olho através da pupila e atinge a retina, onde células fotorreceptoras percebem a luz e cor. W.Stanley Stiles e B.H. Crawford estudaram o fenômeno no qual o brilho medido diminui conforme a luz entra distante do centro da pupila (Ver a figura).
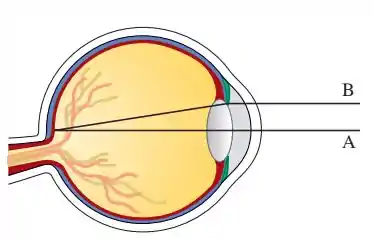
O raio de luz A que entra através do centro da pupila possui maior brilho em relação ao raio B entrando no canto da pupila.
Eles detalharam seus descobrimentos deste fenômeno, conhecido como o Efeito de Stiles-Crawford, em um importante artigo publicado em 1933. Em particular, eles observaram que a quantidade de luminosidade sentida não era proporcional a área da pupila como eles esperavam. A porcentagem P do total de luminosidade que entra na pupila de raio r mm que é sentida pela retina pode ser descrita por
Onde é uma constante experimental, de valor 0,05.
(a) Qual a porcentagem de luminosidade sentida por uma pupila de raio 3mm?
(b) Calcule a porcentagem de luminosidade sentida por uma pupila de raio 2mm. Faz sentido que ela seja maior que a resposta da letra (a)?
(c) Calcule O resultado é o esperado? Este resultado é fisicamente possível?
Passo 1
Oiee, vamos lá?
Na resolução deste problema, a teoria usada envolveu o entendimento do fenômeno físico estudado pelos pesquisadores W. Stanley Stiles e B.H. Crawford, conhecido como o Efeito de Stiles-Crawford.
Eles observaram que a quantidade de luminosidade sentida pela retina não era proporcional à área da pupila, como esperado, e formularam uma expressão matemática para descrever a porcentagem do total de luminosidade que entra na pupila de raio que é sentida pela retina.
Essa expressão é dada por:
Onde:
- é uma constante experimental, com valor
Essa expressão modela como a quantidade de luminosidade sentida pela retina varia em relação ao raio da pupila.
Para resolver as partes do problema, aplicamos essa teoria, substituindo os valores fornecidos na expressão e realizando os cálculos correspondentes.
Na parte encontramos a porcentagem de luminosidade sentida por uma pupila de raio
Na parte fizemos o mesmo para uma pupila de raio
E na partecalculamos o limite quando o raio da pupila tende a o que nos dá uma indicação do comportamento da luminosidade sentida quando a pupila se aproxima de um tamanho muito pequeno.
Ao aplicar essa teoria, pudemos entender como a quantidade de luminosidade percebida varia em relação ao tamanho da pupila e como isso afeta a visão humana.
Passo 2
Bom pessoal, a equação que rege a porcentagem da luminosidade total que entra na pupila é dada por:
(a) Para uma pupila de 3 mm, temos que substituir este valor na equação:
Passo 3
(b) Para uma pupila de 2 mm:
Este resultado faz sentido, pois como a pupila é menor, sua área é mais concentrada no centro da pupila, região que a luminosidade é mais sentida pela retina.
Quanto maior for a pupila, haverá regiões maiores que recebem luminosidade, mas que são pouco sentidas pela retina, o que faz a porcentagem diminuir para pupilas maiores.
Passo 4
(c) Para encontrar o limite, devemos substituir o valor:
Temos então uma indeterminação. Para resolver isto, podemos aplicar a regra de L’Hopital, derivando em cima e embaixo de forma isolada:
Voltando para o limite:
Substituindo o valor do limite:
Quando a pupila tende a um raio muito pequeno, então ela somente receberá luz no seu centro, região que a retina melhor percebe a luminosidade.
Entretanto, é impossível que a retina perceba toda a luminosidade da pupila, pois parte desta luminosidade irá ser perdida mesmo dentro do olho.