Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.7 - Ex. 13

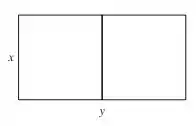
Um fazendeiro quer cercar uma área de 15   000   m 2 em um campo retangular e então dividí-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma a minimizar o custo da cerca?

Passo 1

Eaee, belezinha?? Bom.. queremos minimizar o custo de uma cerca de forma que temos que cercar uma área de 15   000   m 2 em um campo retangular e então dividí-lo ao meio com uma cerca paralela a um dos lados do retângulo.

Ficou difícil de imaginar? Pois se liga na figura abaixo:

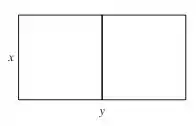
Bom... para a gente fazer isso, temos que relacionar a área desse retângulo com o perímetro e aplicar conceitos de maximização/minimização através de derivadas.

Bora lá?? 😉

Passo 2

Então... Do enunciado, a gente temque a área total é de 15000   m 2 .

Assim, de acordo com a figura, temos:

x y = 15000 ∴

x = 15000 y

E ainda pela figura a gente tem que o perímetro é a onde a gente vai inserir a cerca, ou seja:

P = 3 x + 2 y

Substituindo x , temos:

P = 45000 y + 2 y ∴

P = 45000 + 2 y 2 y

Passo 3

Para encontrarmos o mínimo de P basta derivarmos e igualar a zero:

P ' = 4 y 2 - 45000 - 2 y 2 y 2 = 2 y 2 - 45000 y 2

Igualando a zero

2 y 2 - 45000 y 2 = 0 ∴

2 y 2 - 45000 = 0 ∴

2 y 2 = 45000 ∴

y 2 = 22500 ∴

y = 150   m

Encontrando x

x = 15000 150 = 100   m

Logo, o perímetro mínimo é

P = 3 ⋅ 100 + 2 ⋅ 150 = 600 m

Entendeu direitinho?? Responde aee 😉

Resposta

O fazendeiro deve delimitar a área com um comprimento de x = 100 m e uma largura de y = 150 m e dividí-la no meio, como mostra a figura

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fazendeiro com 750 pés de cerca quer cercar uma área retangular e então dividi-la em quatro partes com cercas paralelas a um lado do retângulo. Qual é a maior área total possível das quatro partes?
Uma caixa de tampa deve ser construída a partir de um pedaço quadrado de papelão, com 3 pés de largura, cortando fora um quadrado de cada um dos quatro cantos e dobrando para cima os lados. Encontre o
39. Se lhe for oferecida uma fatia de uma pizza redonda (em outras palavras, um setor de um círculo) e a fatia precisar ter um perímetro de 60 cm, qual diâmetro da pizza vai recompensá-lo com a maior
Se os dois lagos iguais de um triângulo isósceles tem comprimento a, encontre o comprimento do terceiro lado que maximiza a área do triangulo.
Responda o exercício 37 se um dos pedaços é dobrado em um quadrado e o outro em um círculo.