Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.8 - Ex. 19
A figura abaixo mostra um dique cuja face é um retângulo inclinado. Encontre a força do fluido sobre a face quando o nível da água estiver no topo do dique.
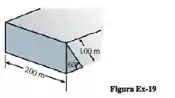
Passo 1
O primeiro passo é verificarmos a figura por um diagrama que demonstra as duas dimensões:
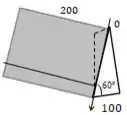
Assim, temos que a altura será dada por .
Sabemos que pelos ângulos internos, o outro vértice forma um ângulo de 30°, logo,
Agora é só substituirmos na formula 8!!
Passo 2
Substituindo, temos:
Resolvendo a integral:
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Aplicar os resultados dos exercícios 9 e 10 para encontrar o menor e o maior valor possível da integral a seguir. ∫ 3 4 5 x d x
∫ 0 3 x x + 1 d x
Aplicar os resultados dos exercícios 9 e 10 para encontrar o menor e o maior valor possível da integral a seguir. ∫ - 1 4 ( x 4 - 8 x 2 + 16 ) d x
∫ 0 4 2 x + 1 - 1 2d x
Aplicar os resultados dos exercícios 9 e 10 para encontrar o menor e o maior valor possível da integral a seguir. ∫ 1 4 | x - 1 | d x