Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 38

Ache o volume do sólido gerado pela rotação da região no primeiro quadrante limitada pela curva e pelos eixos coordenados em torno do eixo y.

Passo 1

Vamos utilizar a imagem abaixo para visualizarmos a região dada no enunciado

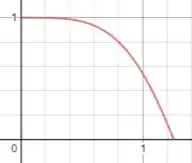
Como faremos a rotação dessa região, vamos usar a equação do volume por invólucro cilíndrico:

Passo 2

Como só temos a própria curva e a rotação é em torno do eixo y, precisamos apenas substituir a curva em f(x) na nossa equação. Os limites de integração serão e, quando a função encosta no eixo x, ou seja quando .

Vamos substituir esse valor na curva:

Então x será:

Nossa equação de volume ficará assim:

Passo 3

Para resolvermos a integral, faremos a seguinte substituição:

Resolvendo primeiro a integral indefinida, ficamos com:

Integrando:

Retornando à variável x:

Aplicando os limites de integração:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o segundo teorema de Pappus descrito no exercício 48 para encontrar a área de superfície do toro do exemplo 7.

Prove as fórmulas 9.

Faça com que R seja uma região que fica entre as curvas: y = x m , y = x n , 0 ≤ x ≤ 1 Onde m e n são inteiros com 0 ≤ nm .a) Esboce a região R .b) Encontre as coordenadas do centróide de R .c) Tente

O centróide de uma curva pode ser encontrado por um processo similar ao usado para encontrar o centróide de uma região. Se C é uma curva com comprimento L , então o centróide é ( x - , y - ) onde x -

O segundo teorema de Pappus está na mesma linha do teorema de Pappus da página 565, mas para área de superfície ao invés de volume: Faça com que C seja a curva que fica inteiramente de um lado de uma