Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 36

Ache o volume do sólido gerado pela rotação da região limitada pela curva x 2 3   +   y 2 3 = a 2 3 em torno do eixo y.

Passo 1

Vamos substituir o valor de a por 1 para que possamos ter um esboço de como é a região para facilitar a compreensão:

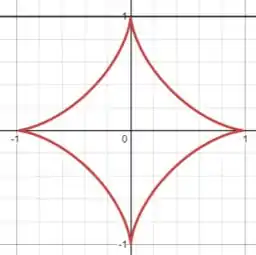
Como a rotação é em torno do eixo y, como a região é simétrica em relação aos dois eixos, vamos pegar apenas o primeiro quadrante para calcularmos o volume e depois multiplicaremos por dois (não por quatro, pois a rotação por 2 π já irá garantir metade do nosso sólido). Usaremos a equação de volume por invólucro cilíndrico:

V = 2 π ∫ b c x f x d x

E escreveremos a equação da curva em termos de x:

y = f x = a 2 3 - x 2 3 3 2

Passo 2

Os limites de integração da região do primeiro quadrante será x = 0 limitado pelo eixo y e x = a limitado pela curva (lembrando que apenas no desenho a = 1 ). Nossa integral então ficará:

V = 2 π ∫ 0 a x a 2 3 - x 2 3 3 2 d x

Passo 3

Resolvendo primeiro a integral indefinida:

V = 2 π ∫ x a 2 3 - x 2 3 3 2 d x

Multiplicando e dividindo por x 1 3 :

V = 2 π ∫   x - 1 3   x 4 3 a 2 3 - x 2 3 3 2 d x

Agora faremos a seguinte substituição:

u = a 2 3 - x 2 3 → d u = - 2 3 x - 1 3 d x

d x = - 3 2 x 1 3 d u

Substituindo na integral ficamos com:

V = 2 π ∫   x - 1 3   ( a 2 3 - u ) 2 u 3 2 - 3 2 x 1 3 d u

Simplificando os termos:

V = - 3 2 . 2 π ∫   ( a 2 3 - u ) 2 u 3 2 d u

Reescrevendo:

V = - 3 π ∫   u 3 2 a 4 3 - 2 u 5 2 a 2 3 + u 7 2 d u

Integrando cada termo:

V =   - 3 π 2 5 u 5 2 a 4 3 - 4 7 u 7 2 a 2 3 + 2 9 u 9 2 + c

Voltando para varável x:

=   - 3 π 2 5 u 5 2 a 4 3 - 4 7 u 7 2 a 2 3 + 2 9 u 9 2 + c

V = -   3 π 3 5 a 2 3 - x 2 3 5 2 a 4 3 - 6 8 a 2 3 - x 2 3 7 2 a 2 3 + 3 11 a 2 3 - x 2 3 9 2 + c

Substituindo os limites de integração, o superior irá zerar cada termo, e o inferior resultará:

V = 3 π 3 5 a 2 3 5 2 a 4 3 - 6 8 a 2 3 7 2 a 2 3 + 3 11 a 2 3 9 2

V = 16 105 π a 3

Multiplicando o resultado por 2 para a outra metade da região:

V = 32 105 π a 3

Resposta

V = 32 105 π a 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . y = x , x = 2 y , s o b r ex = 5
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = - 3 y 2 + 12 y - 9 , x = 0
29-32.Cada integral representa o volume de um sólido. Descreve o sólido.32. ∫ 0 1 2 π 2 - x 3 x - 2 x d x
33-34 Use o gráfico para estimar a abscissa dos pontos de inteerseção das curvas dadas. Então use essa informação e sua calculadora para estimar o volume do solido obtido pela rotação sobre o eixo y d
33-34 Use o gráfico para estimar a abscissa dos pontos de inteerseção das curvas dadas. Então use essa informação e sua calculadora para estimar o volume do solido obtido pela rotação sobre o eixo y d