Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 39
A região no primeiro quadrante, limitada pela curva pelo eixo y, e pelo eixo x, onde gira em torno do eixo x. Ache o volume do sólido gerado.
Passo 1
Vamos utilizar a imagem abaixo para visualizarmos a região que é falada no enunciado:
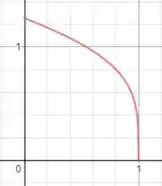
Como é pedido o volume do sólido gerado pela rotação da região acima, vamos utilizar a equação de volume por invólucro cilíndrico:
Passo 2
Como a curva que o enunciado nos deu, está escrita em termos de y, precisamos encontrar os valores de y para os quais , com isso obteremos os limites de integração:
E para
Nossa integral então vai ficar:
Passo 3
Faremos a seguinte substituição para resolvermos a integral:
Primeiro fazendo a integral indefinida:
Substituindo y:
Integrando:
Retornando à variável y:
Substituindo os limites de integração:
Resposta
Exercícios de Livros Relacionados
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x + y = 4 , x = y 2 - 4 y + 4
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . y = 4 - 2 x , y = 0 , x = 0 ; s o b r ex = - 1
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = 2 y 2 , y ≥ 0 , x = 2 , s o b r ex = 2
Use o método de cascas cilíndricas para induzir o volume gerado girando a região delimitada pelas curvas dadas sobre o eixo especificado. y = x 3 , y = 8 , x = 0 ; s o b r ex = 3
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = 2 y 2 , x = y 2 + 1 , s o b r ey = - 2