Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 41

Um buraco com cm de raio é feito através do centro de um sólido esférico com 4 cm de raio. Ache o volume da parte do sólido que foi cortada fora.

Passo 1

Certo, vamos fazer um esboço de apenas uma fatia da esfera, onde o furo está no eixo y, cruzando a esfera toda:

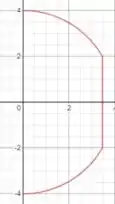
Ao fazermos a rotação dessa região em torno do eixo y, obteremos a região onde o buraco está ao fazerem um buraco na esfera. Para fazermos essa rotação, utilizaremos a equação de volume por invólucro cilíndrico:

Passo 2

Vamos montar a equação para essa região que é, de certa forma, um pedaço de uma circunferência, e, portanto, nossa equação pode ser a seguinte:

Vamos reescrevê-la em termos de x:

Para expressarmos essa função na equação da integral, e integrarmos a parte onde y é negativo, utilizaremos o módulo da função multiplicada por 2, ficamos com:

Os limites de integração serão desde origem , até o final do raio do furo .

Nossa integral então ficará:

Passo 3

Resolvendo a integral através da seguinte substituição:

Ficaremos com a seguinte integral indefinida:

Integrando:

Retornando à variável x:

Substituindo os limites de integração:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo y da região limitada pelas curvas dadas. Esboce a região e a casca típica. y = 3 + 2 x - x 2 , x + y = 3

Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo y da região limitada pelas curvas dadas. Esboce a região e a casca típica. y = 4 x - 2 2 , y = x 2 - 4 x +

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica. y = x 2 , y = 0 ,

Use um gráfico para estimar as coordenadas de x dos pontos de interseção das curvas dadas. Então use essa informação para estimar o volume do solido obtido pela rotação ao redor do eixo y da região li

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica. y = x - 1 , y = 0