Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 40
Um buraco com 2 cm de raio é feito através de um sólido esférico de 6 cm de raio e o eixo do buraco é um diâmetro da esfera. Ache o volume da parte que sobra da esfera.
Passo 1
Certo, vamos fazer um esboço de apenas uma fatia da esfera, onde o furo está no eixo y, cruzando a esfera toda:
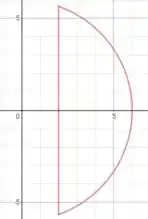
Ao rotacionarmos essa região inteira, vamos obter o volume da esfera em torno do eixo y. Usaremos a equação de volume por invólucro cilíndrico:
Passo 2
Primeiro precisamos escrever uma função que descreva a nossa região, como é uma parte de uma circunferência de raio 6 cm, vamos escrever a equação para a circunferência:
Reescrevendo em termos de x, ao fazermos isso, a função deveria ser escrita da seguinte forma:
Para considerarmos a parte negativa e a parte positiva da função na integral, para que todo o semi-círculo seja integrado, vamos precisar multiplicar por dois o módulo de f(x). Ficamos então com:
Os limites de integração vão desde o raio do buraco até o raio da esfera, então nossa equação de volume ficará:
Passo 3
Resolvendo primeiro a integral indefinida:
Faremos primeiro a substituição:
Nossa integral fica:
Integrando:
Voltando para x:
Substituindo os limites de integração: