Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.1 - Ex. 40
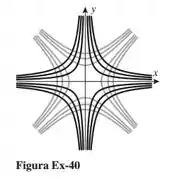
A Figura Ex-40 mostra alguns membros típicos das famílias de hipérboles (curvas pretas) e (curvas cinzas), onde e . Use a sugestão do Exercício 39 para mostrar que essas famílias são trajetórias ortogonais uma da outra.
Passo 1
Queremos provar que cada membro da família é ortogonal a cada membro da família .
Para fazer isso a gente pode usar a sugestão do enunciado e verificar que nos pontos de interseção, as retas tangentes são perpendiculares entre si.
E isso quer dizer que as inclinações das retas tangentes:
tem essa relação nos pontos em comum:
E para chegar em , precisamos derivar essas equações implicitamente, belezinha?
Vamos começar!
Passo 2
Vamos achar a inclinação da reta tangente para a família . Derivando essa equação dos dois lados:
A derivada de é zero, porque ele é uma constante.
Sabemos que é uma função de , então em temos o produto de duas funções. Usando a regra do produto ali:
Agora a gente isola para achar :
Conseguimos!
Passo 3
Vamos agora achar a inclinação da reta tangente para a família Derivando dos dois lados:
A derivada de é zero, porque ele é constante.
Repara também que como é função de , a derivada de é a derivada de uma função composta, então vamos precisar usar a regra da cadeia:
Isolando para chegar em :
Passo 4
Agora vamos comparar as duas inclinações:
Vamos testar em:
Bate certinho!
Isso diz para gente que as retas tangentes vão ser ortogonais nesses pontos, o que prova que essas famílias são trajetórias ortogonais uma da outra, como o enunciado pediu. 😊
Resposta
Prova nos passos.