Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.9 - Ex. 1

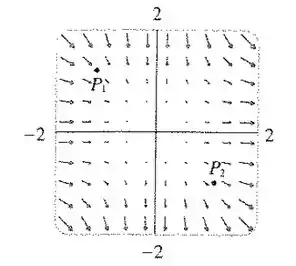
A figura mostra um campo vetorial . Use a interpretação da divergência derivada nesta seção para determinar se div é positivo ou negativo em e em .

Passo 1

Fala ai galera , o exercício quer que a gente diga se o div é positivo ou negativo em e em através da interpretação da divergência derivada.

A ideia da divergência é a mesma para quando traçamos linha de campo elétrico em carga positiva e negativa na física.

Quando temos uma carga positiva as linhas de campo elétrico saem da carga e nas de carga negativa as linhas de campo elétrico tendem a entrar. Nisso ignora os vetores que tendem a fazer um movimento contrário a esses (pois eles são bem menores).

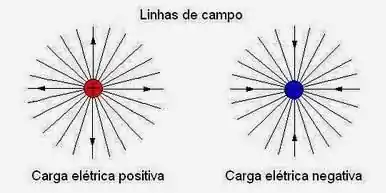
Sabendo dessa explicação vamos avaliar as linhas do campo vetorial usando a teoria acima, beleza?

Passo 2

Relembrando que nosso campo vetorial é:

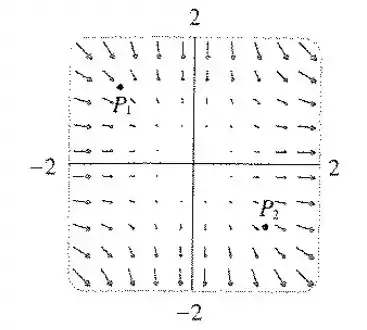
Com raciocínio anterior vemos que em as linhas entram nele, sendo uma divergência negativa e na mesma figura vemos que as linhas saem de sendo então uma divergência positiva.

O que deve ser observado aqui é que os vetores que entram em são maiores do que os que saem, sobressaindo os vetores maiores. E os vetores que entram em são menores do que os que saem, e é para eles que vamos observar.

Logo podemos dizer que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11. Seja F o campo do exercício anterior e seja γ t = cos ⁡ t , sin ⁡ t 0tπ 2 Calcule ∫ γF ⋅ n d S Onde n é a normal com componente y0(Sugestão. Escolha um compacto K conveniente e aplique o teorema d

13. Seja f x , y = x 3 ,- 3 x 2 y , γ 1 = t ,e t 2 - 1 ,0 ≤ t ≤ 1 e γ 2 = t , t 2 ,0 ≤ t ≤ 1 . Seja, n 1 a normal de γ 1 com componente y0 e n 2 a normal de γ 2 com componente yCalcule ∫ γ 1F ⋅ n d S

Seja v : Ω ⊂ R 2 → R de classe C 2 no aberto Ω e sejam γ e K como no exercício anterior. Prove que se ∇ 2 v = 0 no interior de K e v γ t = 0 em a , b , então v x , y = 0 para todo x , y ∈ K . Suponha,

Seja F → x , y = x 3 y 3 i → + 3 y - 3 4 x 2 y 4 j → e seja y t = t 3 ,s e n 4 arctan ⁡ t 2 ,0 ≤ t ≤ 1 .Seja α a área do conjunto limitado pelo eixo x e pela curva γ . ∫ γ F →⋅ n →d s onde n → é a nor

Sejam γ e K como no exercício 8 . Seja F x , y uma função a valores reais definida e contínua no interior de K e seja f x uma função a valores reais definida e contínua em ] a , b [ . Considere o prob