Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.4 - Ex. 10

Seja F → x , y = x 3 y 3 i → + 3 y - 3 4 x 2 y 4 j → e seja y t = t 3 ,   s e n 4 arctan ⁡ t 2 ,   0 ≤ t ≤ 1 .

Seja α a área do conjunto limitado pelo eixo x e pela curva γ . ∫ γ F →   ⋅ n →   d s onde n → é a normal a γ e que aponta para fora do conjunto acima mensionado

Passo 1

A área que o nosso enunciado se refere é

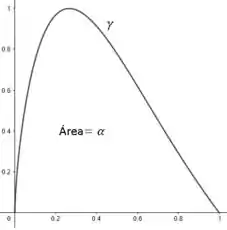
Temos que, suponha que γ seja regular e injetora (ver inicio da Sesão 8.4 ). Então podemos considerar os campos vetoriais dados por

n → γ t = 1 γ ' t y ' t i → - x ' t j → , a < t < b

e

n → 2 y t = - n → 1 y t .

Passo 2

Primeiro, se observarmos bem nossa γ e o Teorema da Divergência, percebemos que não podemos aplica-lo, pois nossa curva não é fechada. Entretanto podemos brincar com nossa integral e criar uma outra γ afim de fechar nossa curva, assim tome

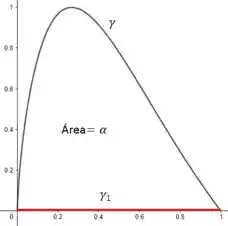
Onde agora podemos escrever que

∫ γ F → ⋅ n →   d s = ∫ γ F → ⋅ n →   d s + ∫ γ 1 F → ⋅ n →   d s - ∫ γ 1 F → ⋅ n →   d s

Onde fazemos que nossa nova γ → γ + γ 1 assim temos que

∫ γ F → ⋅ n →   d s = ∮ γ F → ⋅ n →   d s - ∫ γ 1 F → ⋅ n →   d s

Agora repare que como γ 1 t , 0 com 0 ≤ t ≤ 1

F γ 1 t = 0

Bonito né ?

Isso quer dizer que

∫ γ F → ⋅ n →   d s = ∮ γ F → ⋅ n →   d s

E aplicando o teorema da divergência

∫ γ F → ⋅ n →   d s = ∮ γ F → ⋅ n →   d s = ∬ α ∇ ⋅ F →   d x   d y

Passo 3

Agora vamos então calcular o nosso divergente

∇ ⋅ F → = ∂ x 3 y 3 ∂ x + ∂ 3 y - 3 4 x 2 y 4 ∂ y = 3 x 2 y 3 + 3 - 3 x 2 y 3 = 3

Assim temos que

∬ α ∇ ⋅ F → d x d y = 3 ∬ α d x d y = 3 α

Perceba que os gráficos em si só ilustraram o que queríamos fazer, mas mesmo sem eles, já seria possível percber a tática que utilizamos para resolver o passo 2.

Resposta

3 α

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.e) v → x , y , z = 2 x z , - 2 y z , 2 z
Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.c) v → x , y , z = 2 x , - 2 y , 0
Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.a) v → x , y = 2 y - 3 i → + x 2 j →
Um fluido escoa em movimento uniforme no domínio D = { x , y 0 ≤ y ≤ 8 } . Se a velocidade em cada ponto é dado por v → = y + 1 i → , verificar que todas as partículas se deslocam em linha reta e que
Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.b) v → x , y , z = x , y , z