Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.4 - Ex. 11

11. Seja F o campo do exercício anterior e seja

γ t = cos ⁡ t , sin ⁡ t

0 < t < π 2  

Calcule

∫ γ   F ⋅ n d S

Onde n é a normal com componente y>0

(Sugestão. Escolha um compacto K conveniente e aplique o teorema dadivergência.)

Passo 1

Primeiro temos que fazer uma errata. Afinal se estamos numa integral de linha não podemos ter um d S ( ou seja uma integração de seperficie ) temos que ter um d r (uma integral de uma única variável, uma linha) , Assim devemos escrever

∫ γ   F ⋅ n d S →   ∫ γ   F ⋅ n d r

Dito isso podemos começar. O campo do exercício anterior é

F = x 3 y 3 ,   3 y - 3 4 x 2 y 4

Passo 2

Podemos usar o teorema da divergência. Que diz

∮ γ F ⋅ n d r =   ∫ ∫ ∇   . F d S

Ou seja temos que ter um contorno fechado para calcular

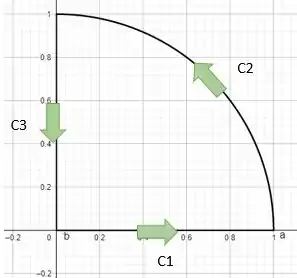
Contudo nossa região que queremos calcular é apenas C2. Então vamos precisar usar de truques para resolver.

Passo 3

Se fossemos parametrizar C2 e integrar teríamos uma conta enorme e não tao trivial em mãos. Podemos então fazer o seguinte usar o teorema da divergência em toda a região fechada

∮ γ F ⋅ n d r =   ∫ ∫ ∇   . F d S

Sendo que

∇   . F = 3 x 2 y 3 + 3 -   3 x 2 y 3  

∇   . F = 3

Logo

∫ ∫ ∇   . F d S =   ∫ ∫ 3 d S

Seria 3 vezes a área da região. Assim

∫ ∫ 3 d S = 3 π 4

Passo 4

Dessa forma

∮ γ ' F ⋅ n d r =   ∮ c 1   F ⋅ n d r + ∮ c 2 F ⋅ n d r + ∮ c 3 F ⋅ n d r = 3 π 4

Como queremos apenas C2 podemos escrever

∮ c 2 F ⋅ n d r = 3 π 4 -   ∮ c 1   F ⋅ n d r -   ∮ c 3   F ⋅ n d r  

Agora so nos resta calcular a nossa função nos eixos coordenados.

Passo 5

Vamos calcular C1

∮ c 1   F ⋅ n d r

Podemos parametrizar F da seguinte maneira

C 1 = t , 0

C 1 ' = 1,0

O que faz com que

F C 1 t = 0,0

Logo podemos concluir que essa integral vai dar nula.

Passo 6

Por fim ,vamos calcular C3

∮ c 3   F ⋅ n d r

Podemos parametrizar F da seguinte maneira

C 3 = 0 , - t

C 1 ' = 0 , - 1

O que faz com que

F C 1 t = 0 , - 3 t

Podemos calcular a normal da seguinte maneira

n = ∇ g ∇ g

Sendo

g   : x = 0

O que faz com que a normal seja

n = ( 1,0 ) 1

Dessa forma

∮ c 3   F ⋅ n d r = ∮ c 3   0 , - 3 t ⋅ 1,0 1 d r → 0

Logo como as curvas C1 e C3 são nula, podemos concluir que

∮ c 2 F ⋅ n d r = 3 π 4

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ γ   F ⋅ n d S = 3 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verifique se o Teorema do Divergente é verdadeiro para o campo vetorial F → na região E . F → x , y , z = x 2 s e nyi ^ + x cos ⁡ yj ^ - x zs e nyk ^ S é a “Esfera gorda” x 8 + y 8 + z 8 = 8 .
Use o Teorema do Divergente para calcular a integral de superfície ∬ c F → ⋅ d S → ; ou seja, calcule o fluxo de F → através de S . F → x , y , z = x 4 i → - x 3 z 2 j → + 4 x y 2 z k → S é a superfíc
Use o Teorema do Divergente para calcular a integral de superfície ∬ c F → ⋅ d S → ; ou seja, calcule o fluxo de F → através de S . F → x , y , z = c o s z + x y 2 i → + x e - z j → + s e n y + x 2 z
Seja F → x , y , z = z tg - 1 ⁡ y 2 i ^ + z 3 ln ⁡ x 2 + 1 j ^ + zk ^ . Determine o fluxo de F → através da parte do paraboloide x 2 + y 2 + z = 2 que está acima do plano z = 1 e está orientada para b
Use o Teorema do Divergente para calcular a integral de superfície ∬ c F → ⋅ d S → ; ou seja, calcule o fluxo de F → através de S . F → x , y , z = x 3 y i → - x 2 y 2 j → - x 2 y z k → S é a superfíc