Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.3 - Ex. 1
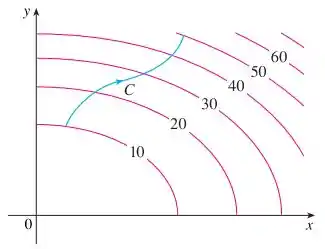
A figura mostra uma curva e um mapa de contorno de uma função cujo gradiente é contínuo. Determine .
Passo 1
Então pessoal, essa questão é apenas pra gente pegar a ideia sobre integrais de linha. A curva que temos é bem suave e contínua, então o valor de vai ser apenas a diferença entre o valor final e o valor inicial da curva de nível.
Passo 2
Se observarmos o gráfico, a curva final está em e a inicial está em , então:
E é esse nosso resultado!
Resposta
Exercícios de Livros Relacionados
Determine uma função f tal que F = ∇ f e b) use a parte a) para calcular ∫ C F ⋅ d r sobre a curva C dada. F x , y = x 3 y 4 i + x 4 y 3 j C : r t = t i + 1 + t 3 j ,0 ≤ t ≤ 1
A partir do gráfico de F você diria que ele é conservativo? Verifique se seu palpite estava correto. F x , y , = 2 x y + sen y i + x 2 + x cos yj
A partir do gráfico de F você diria que ele é conservativo? Verifique se seu palpite estava correto. F x , y , = x - 2 y i + x - 2j 1 + x 2 + y 2
Determine o trabalho realizado pelo campo vetorial de força F movendo um objeto um objeto de P a Q. F x , y = y 2 x 2 i - 2 y x j ;P 1,1 ,Q ( 4 , - 2 )
Determine uma função f tal que F = ∇ f e b) use a parte a) para calcular ∫ C F ⋅ d r sobre a curva C dada. F x , y = y i + x + 2 y j , C é a semicircunferência superior que começa em (0,1) e termina e