Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.3 - Ex. 25

A partir do gráfico de F você diria que ele é conservativo? Verifique se seu palpite estava correto.

F x , y , = x - 2 y i + x - 2   j 1 + x 2 + y 2

Passo 1

Seja F x , y = P x , y i + Q x , y j . Para checarmos se esse campo vetorial é conservativo, basta verificarmos se:

∂ P ∂ y = ∂ Q ∂ x

E é isso o que precisamos fazer.

Entretanto, antes disso, vamos começar esboçando o nosso campo vetorial e tentar analisar se ele será conservativo ou não. Sendo assim, vejamos o campo vetorial abaixo.

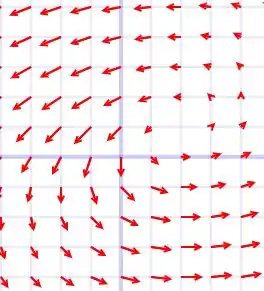
É esperado que o campo não seja conservativo, pois podemos desenhar curvas fechadas e cujos vetores estão na mesma direção que a nossa curva. Por exemplo, circunferências centradas na origem.

Passo 2

Agora, vamos verificar se nosso palpite esta certo ou não. Basta calcularmos as derivadas parciais conforme dita no Passo 1. Logo, temos:

∂ P ∂ y = - 2 ⋅ 1 + x 2 + y 2 - x - 2 y ⋅ y 1 + x 2 + y 2   ( 1 + x 2 + y 2 )

∂ P ∂ y = - 2 ⋅ ( 1 + x 2 + y 2 ) - x y - 2 y 2   1 + x 2 + y 2 ⋅ ( 1 + x 2 + y 2 ) = - 2 - 2 x 2 - x y 1 + x 2 + y 2 3 / 2

Continuando, temos:

∂ Q ∂ x = 1 ⋅ 1 + x 2 + y 2 - x - 2 ⋅ x 1 + x 2 + y 2   ( 1 + x 2 + y 2 )

∂ P ∂ y = ( 1 + x 2 + y 2 ) - x 2 - 2 x   1 + x 2 + y 2 ⋅ ( 1 + x 2 + y 2 ) = 1 + y 2 - 2 x 1 + x 2 + y 2 3 / 2

Como

∂ P ∂ y ≠ ∂ Q ∂ x

Temos que o campo F não é conservativo! E assim, confirmamos a nossa hipótese.

Resposta

O campo não é conservativo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f um campo escalar e F um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar. r o tf g r a df d
Existe um campo vetorial G → em R 3 tal que rot ⁡ G → = x y z , - y 2 z , y z 2 ? Explique.
Existe um campo vetorial G → em R 3 tal que rot ⁡ G → = x sen ⁡ y , cos ⁡ y , z - x y ? Explique.
Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = y e - xi + e - x j + 2 zk
Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = e zi + j + x e zk