Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.8 - Ex. 1
A figura mostra o gráfico da função . Suponha que seja usado o método de Newton para aproximar a raiz da equação com como aproximação inicial.
(a) Desenhe as tangentes que são usadas para encontrar e , e estime os valores numéricos de e .
(b) Uma melhor aproximação seria ? Explique.
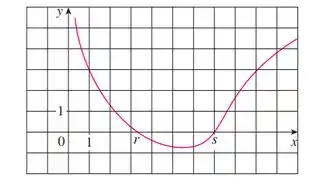
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente o gráfico de uma função , dado por:
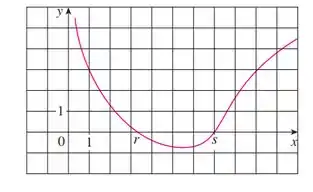
Teremos que supor que seja usado o método de Newton para aproximar a raiz da equação
com
como aproximação inicial.
O que teremos que fazer aqui é:
No item (a), desenhar as tangentes que são usadas para encontrar e , e estime os valores numéricos de e .
Para isso, precisamos lembrar que no método de Newton vamos considerar uma reta tangente à curva da função no ponto .
Depois devemos procurar a interseção de como o eixo , que será chamada de e verificar o quão próximo está da interseção da curva com o eixo .
Para encontrar , podemos fazer:
Depois, repetimos o processo, usando como uma segunda aproximação, fazendo:
E podemos repetir o processo quantas vezes for necessário. De modo geral, fazendo
E se ficar cada vez mais próxima da raiz de nossa curva à medida que cresce, fizemos que a sequência converge para .
Assim:
Perfeito.
E no item (b), precisamos dizer se uma melhor aproximação seria . Devemos explique nossa resposta.
Então, vamos nessa.
Passo 2
Item (a). Desenhando a reta tangente ao gráfico da função no ponto , teremos:
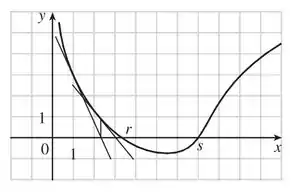
Veja que essa reta tangente em intercepta o eixo em
Então, traçando outra reta tangente em , vemos que ela intercepta o eixo em , então
Passo 3
No item (b), temos que se não teríamos uma melhor primeira aproximação que já que a linha tangente é quase horizontal. E isso com que sua interseção com o eixo ficasse muito distante da realidade.
Na verdade, a segunda aproximação para parece estar à esquerda de .
Resposta
a)
b)
Se não teríamos uma melhor primeira aproximação que já que a linha tangente é quase horizontal. E isso com que sua interseção com o eixo ficasse muito distante da realidade.