Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.1 - Ex. 1
Um tanque com capacidade para galões de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em galões) após minutos.
- Se for o ponto sobre o gráfico de , encontre as inclinações das retas secantes , onde é o ponto sobre o gráfico correspondente a .
- Estime a inclinação da reta tangente em pela média das inclinações de duas retas secantes.
- Use o gráfico da função para estimar a inclinação da reta tangente . (Essa inclinação representa a taxa segundo a qual a água flui do tanque após minutos).
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada uma tabela de valores do volume de um tanque em galões em função do tempo em minutos.
Veja só!
A partir dessa tabela, definimos o ponto em e no item a) nosso objetivo é obter a inclinação da reta secante onde são os pontos em que .
No item b) queremos determinar a inclinação da reta tangente em a partir das inclinações das retas secantes próximas a .
E no item c) queremos esboçar o gráfico da função e estimar a inclinação da reta tangente em .
Parece complicado?
Veja só... para resolver o item a) vamos aplicar uma formulinha que determina a inclinação de uma reta que liga dois pontos.
Essa formulinha é dada por
Onde no caso, como nossa abscissa é o tempo e a ordenada é o volume , temos
Para obter o resultado do item b) pegamos as inclinações mais próximas de (no caso em e ) e calculamos a média entre elas.
Por fim, no item c) temos que esboçar o gráfico da função a partir da tabela e estimar a inclinação da reta tangente no ponto .
Bora começar!
Passo 2
Vamos começar resolvendo o item a) a partir da formulinha que vimos no passo 1...
Para refrescar a memória, vamos trazer a tabela novamente.
Em todos os casos, temos que e
Em , temos que , ou seja
Agora em , temos que , portanto
Seguindo esse método, chegamos para cada as inclinações obtidas na tabela abaixo...
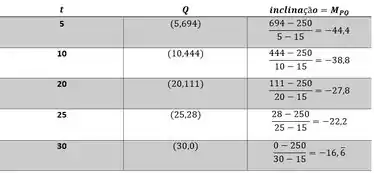
Tranquilo até aqui?
Passo 3
Para o item b) podemos estimar a inclinação da reta tangente em pela média de duas retas secantes em e .
A partir da tabela que construímos no passo 2, vemos que
Como a média entre dois números é a soma desses números divididos por , chegamos em
Show? 😁
Passo 4
Agora no item c) vamos construir o gráfico de esboçando os pontos dados e ligando-os...
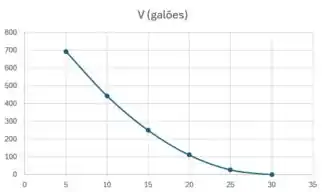
A partir desse gráfico podemos esboçar a reta tangente em
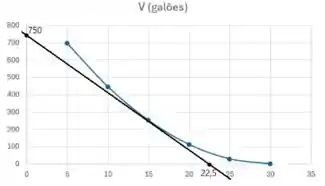
Perceba que a reta corta o eixo das abscissas em e o eixo das ordenadas em , aproximadamente.
A partir da equação que usamos no item a) podemos estimar a inclinação da reta tangente em como
Prontinhoo! O que achou? Responde Aí!
Resposta
