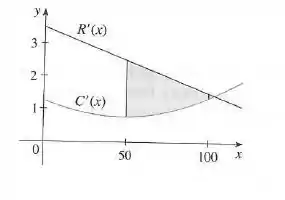
A figura mostra os gráficos da função receita marginal e da função custo marginal de um fabricante. [Lembre-se de que, da Seção , e representam a receita e o custo quando unidades são manufaturadas. Suponha que e são medidos em milhares de dólares.] Qual o significado da área da região sombreada? Use a Regra do Ponto Médio para estimar o valor dessa quantidade.

Sabemos que a curva de representa a mudança da receita e que a curva de representa a mudança do custo. Dessa forma, a área entre as curvas representa a diferença entre Receita e Custo, que é o Lucro.

Utilizando a regra do ponto médio com , temos