Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 34

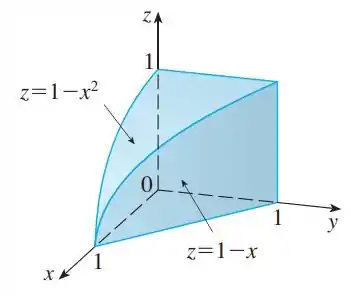
A figura mostra a região de integração da integral

∫ 0 1 ∫ 0 1 - x 2 ∫ 0 1 - x f x , y , z   d y d z d x

Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.

Passo 1

Então, galerinha, nessa questão nós basicamente vamos reescrever essa integral mudando a ordem de integração com seus respectivos limites. Vamos começar!

Podemos isolar o x em z = 1 - x 2 e temos

x = 1 - z

E podemos dizer que

∫ 0 1 ∫ 0 1 - x 2 ∫ 0 1 - x f x , y , z   d y d z d x = ∫ 0 1 ∫ 0 1 - z ∫ 0 1 - x f x , y , z   d y d x d z

Repara que só invertemos a ordem de integração de x   e z

Passo 2

Olhando para integral que o problema forneceu, podemos colocar a variação em y como a mais externa. Com isso temos que deixar os limites de integração de x em função de y .

Pelo gráfico, temos que

0 ≤ x ≤ 1 - y

0 ≤ y ≤ 1

Com isso a nossa integral fica assim,

∫ 0 1 ∫ 0 1 - y ∫ 0 1 - x 2 f x , y , z   d z d x d y

Passo 3

Podemos agora inverter apenas d x   e d y , na integral que encontramos no P a s s o   2 . Fica assim,

∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x 2 f x , y , z   d z d y d x

Passo 4

Agora para x ser o primeiro diferencial, vamos ter que dividir a integral em 2 , uma com 0 ≤ x ≤ 1 - z e outra com 0 ≤ x ≤ 1 - y e na intersecção dos dois temos

1 - z = 1 - y

y = 1 - 1 - z

Ou

1 - z = 1 - y 2

1 - z = 1 - 2 y + y 2

z = 2 y - y 2

E podemos ter

= ∫ 0 1 ∫ 0 1 - 1 - z ∫ 0 1 - z f x , y , z   d x d y d z + ∫ 0 1 ∫ 1 - 1 - z 1 ∫ 0 1 - y f x , y , z   d x d y d z

E

= ∫ 0 1 ∫ 0 2 y - y 2 ∫ 0 1 - y f x , y , z   d x d z d y + ∫ 0 1 ∫ 2 y - y 2 1 ∫ 0 1 - z f x , y , z   d x d z d y

Todas as integrais encontradas levam ao mesmo resultado, ou seja, são iguais!

Resposta

∫ 0 1 ∫ 0 1 - x 2 ∫ 0 1 - x f x , y , z   d y d z d x = ∫ 0 1 ∫ 0 1 - z ∫ 0 1 - x f x , y , z   d y d x d z

= ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x 2 f x , y , z   d z d y d x = ∫ 0 1 ∫ 0 1 - y ∫ 0 1 - x 2 f x , y , z   d z d x d y

= ∫ 0 1 ∫ 0 1 - 1 - z ∫ 0 1 - z f x , y , z   d x d y d z + ∫ 0 1 ∫ 1 - 1 - z 1 ∫ 0 1 - y f x , y , z   d x d y d z

= ∫ 0 1 ∫ 0 2 y - y 2 ∫ 0 1 - y f x , y , z   d x d z d y + ∫ 0 1 ∫ 2 y - y 2 1 ∫ 0 1 - z f x , y , z   d x d z d y

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva cinco outras integrais iteradas que sejam iguais à integral iterada dada. ∫ 0 1 ∫ 0 x 2 ∫ 0 y f x , y , zd z d y d x
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. x = 2 ,y = 2 ,z = 0 ,x + y - 2 z = 2
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. y = 4 - x 2 - 4 z 2 ,y = 0
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. y = x 2 ,z = 0 ,y + 2 z = 4