Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 28
Trace o campo de vetores gradientes de junto com um mapa de contorno de . Explique como eles estão relacionados entre si.
Passo 1
Esse exercício nos pede duas coisas: Primeiro ele quer que determinemos o campo vetorial para depois o compararmos com as curvas de nível.
Para determinarmos o campo vetorial, devemos tomar o gradiente da função , ou seja,
Lembrando que o gradiente de uma função é definido por um vetor, cujas as componentes são as derivadas parciais em cada direção, ou seja
Passo 2
Vamos tomar inicialmente a derivada de na direção .
E na direção temos
Desta forma escrevemos que
Passo 3
Agora precisamos construir o campo vetorial e as curvas de nível .
Esse tipo de campo e curva são muito complicados de desenharmos na mão então o exercício sugere a utilização de um software para construí-los.
Esboçando através de um CAS ficaria assim:
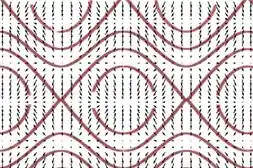
Através do gráfico podemos dizer que o vetor gradiente e as curvas de níveis são perpendiculares entre si. Temos também que o vetor gradiente aponta na direção de .